第二十二章:地基沉降有限元分析
本例将演示如何使用有限元方法模拟超载作用下的地基沉降问题
例题源文件下载地址(v18及以上版本才能打开):http://pan.baidu.com/s/1c1JZPmC
22.1任务
计算长度为 4m,大小为 q = 250kPa 的条形超载所引起的地基沉降,以及移除超载之后的地基沉降变化。地层剖面是各项同性的,岩土材料的参数如下:
表22.1 岩土材料参数
| 天然重度 | γ = 19.0kN/m3 |
| 弹性模量 | E = 15.0MPa |
| 泊松比 | ν = 0.35 |
| 粘聚力 | Cef = 8.0kPa |
| 内摩擦角 | φef = 29.0° |
| 饱和重度 | γsat = 21.0kN/m3 |
考虑到要使用修正弹性模型,还需要输入的岩土材料参数如下:
- 变形模量: Edef = 15.0MPa
- 回弹模量: Eur = 45.0MPa
结论中将对比各种材料本构模型下的地基沉降变形 dZ[mm](这里我们不考虑适用于粘性土的Clam-Clay 模型和亚塑性模型,因为本例中采用的岩土材料为无粘性土)。
注:在实际工程应用中,莫尔-库伦模型(MC)和 Drucker-Prager 模型(DP)也常常用于粘性土, 因为这两种模型都是基于莫尔-库伦剪切破坏理论的,且岩石和土体输入的强度参数相同(φ,c)。
22.2计算
我们使用“GEO5 岩土工程有限元分析计算模块”(以下简称“有限元模块”)(v18 版)来分析该题。以下为建模和分析步骤:
- 建模阶段:分析设置和几何建模
- 工况阶段[1]:初始地应力分析
- 工况阶段[2]:加入超载,分析地基沉降
- 工况阶段[3]:移除超载,分析地基沉降
- 结论
建模阶段:分析设置和几何建模
首先,我们先打开「分析设置」界面,设置“项目类型”、“分析类型”及“初始地应力场的计算方法”。
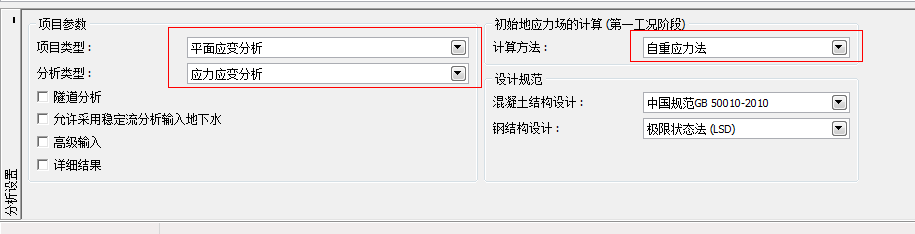
图22.1 「分析设置」– 项目类型;初始地应力场计算
不勾选“隧道模块”、“允许采用稳定流分析输入地下水”、“高级输入”和“详细结果”复选框,这些功能主要是为有丰富有限元建模经验的用户或解决其他某些特定问题而设计的。关于这些功能的介绍在其他章节中会有所讲解,但是更深入的说明则已经超出了本工程设计手册的范围。
注:平面应变分析(平面应变假设)适合解决线性结构问题(例如,隧道、路堤、基坑、大坝等)。 线性结构的特点是其一个方向上的尺寸远大于其他两个方向的尺寸,因此,可以假设这些结构在大尺 寸方向(纵向)的应变为零。该算例采用平面应变假设进行分析(详细信息见帮助文档 - F1)。其他 “项目类型”(轴对称分析)会在接下来的章节中予以讲解。
注:“分析类型”中的“应力应变分析”主要用于分析模型的应力应变,这是最基本的“分析类 型”;其他“分析类型”选项(渗流,边坡稳定分析)会在其他章节分别介绍。
注:软件提供了两种计算初始地应力场的方法(初始地应力场在工况阶段[1]中计算):
“自重应力法”:这是分析初始地应力的标准方法,通过弹性理论来考虑岩土体的竖向应力和水平应力的关系。自重应力法中的侧压力系数由下式给出:
“侧压力系数K0法”(根据Jáky理论,适用于超固结土等土体),该法允许用户自定义侧压力系数的值。
对于当前问题,我们选择莫尔-库伦弹塑性模型作为岩土材料模型(选用其他不同模型的计算结 果对比会在本章的最后给出)。该非线性模型可以得到岩土体中塑性应变和潜在破坏区域的分布。
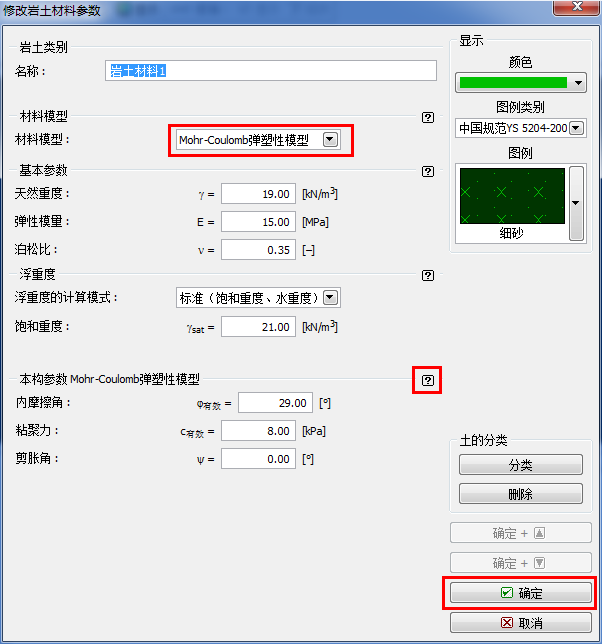
图22.2 设置岩土材料参数
注:线弹性模型假设土的变形遵守胡克定律(理想弹性材料)。该模型的主要优势在于总是可以 得到收敛的结果。但是,只有当超载非常小时,土体的变形才是弹性的,所以弹性模型并不能适用于大部分的实际工程问题。另一方面,对于我们认为不会发生塑性变形的区域,我们可以采用弹性模型 来模拟(例如石笼网挡土墙,刚性地基等),也可以采用弹性模型来验证一个基本的数值模型的正确 性。
注:修正线弹性模型允许岩土体在加载和卸载过程中表现出不同的弹性性质(弹性模量,回弹模量),但是,更理想的结果往往需要采用更复杂的本构模型才能得到,例如,莫尔- 库伦模型、Drucker-Prager 模型。这些模型可以更好地反映岩土体的塑性变形。
下面一步是设置全局坐标范围(所要解决问题的数值模型尺度)和多段线。我们选用的全局坐标 范围要足够大,这样才能使得计算结果不会受到模型边界的影响。对于该算例,选择模型尺度为<-15m, 15m>,设置要计算的土层深度为 15.0m。设置多段线的上的一个坐标为[0,0]的点,点击“确定”,软件会自动添加一条通过该点的水平多段线。
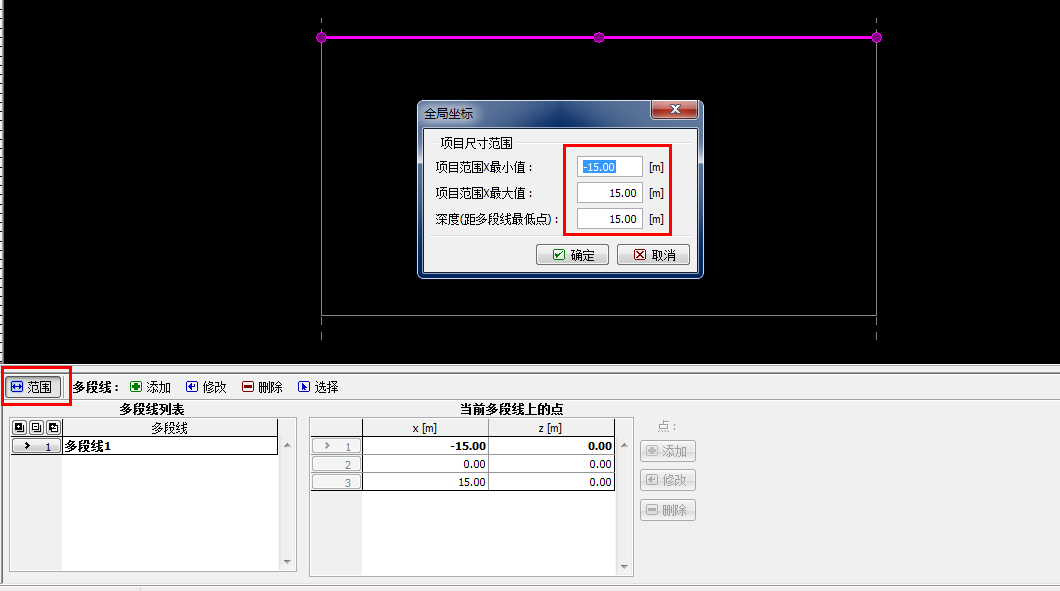
图22.3 设置地表形状 – 输入多段线上的点,全局坐标范围
注:各种岩土工程问题的模型边界范围建议值已在帮助文档中给出(详细信息见帮助文档 - F1)接下来,在「指定材料」界面中赋值模型的岩土材料。直接跳过「接触面类型」、「自由点」、「自 由线」等界面,该算例中不需要使用这些功能。
下一步是生成有限元网格。在该算例中选择网格边长为 1.0m(网格边长的确定取决于要解决问题的尺度和问题的类型)。勾选“网格平滑”复选框,然后点击“启动网格生成”按钮,软件会自动生成平滑的网格。生成网格后,还需要检查一下生成的网格密度对于要解决的问题是否足够大。
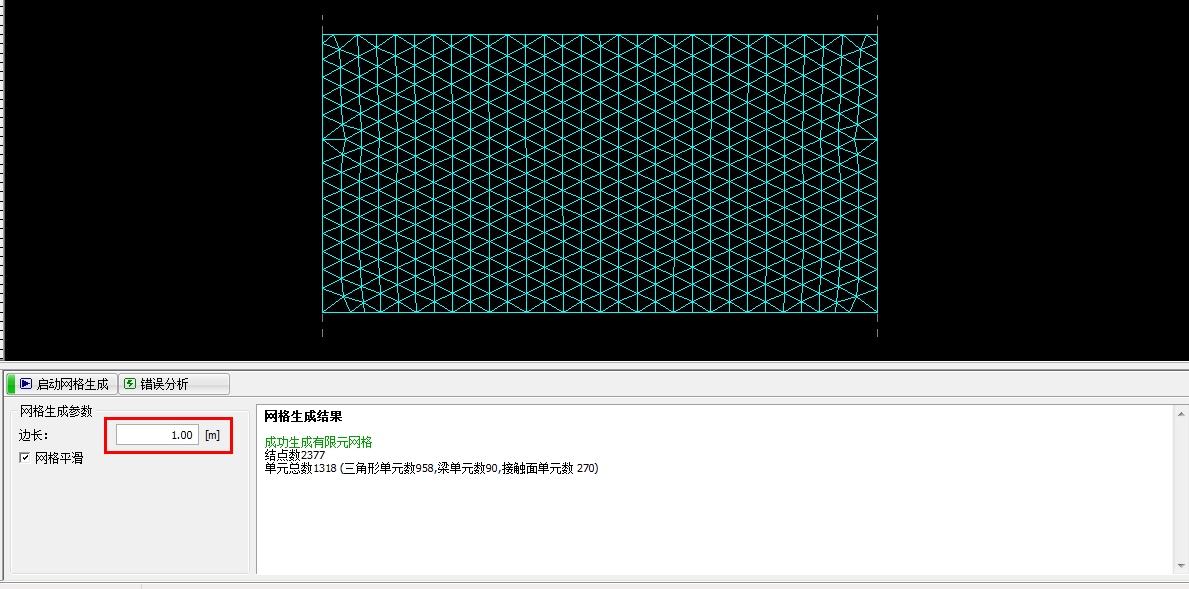
图22.4 生成网格 – 三角形网格
注:标准的 6 节点三角形网格适合于绝大部分的岩土工程问题。若在「分析设置」界面中勾选“高 级输入”复选框,软件还允许生成其他类型的网格(混合网格、3 节点三角形网格),这些选项仅建 议经验丰富的有限元用户使用。
注:生成合理的网格是得到正确计算结果的一个基本条件,因为合理的网格才能反映岩土体的真 实变形情况。网格划分结果会大大影响变形计算结果,而有限元是通过计算出各个网格节点的位移来 推导出其他变量的(应力,应变)。
然而,因为不同的问题差异很大,不可能存在一种确定网格密度的统一原则。对于使用有限元分 析方法的初学者,我们推荐首先使用一个密度较小的网格(边长较大),分析得到结果后,再尝试使 用“网格平滑”等其他几个选项来改变网格(还可以围绕某个点或者某条线来加密或者稀疏网格–详 细使用方法请见本手册的其他相关章节)。通常来说网格密度越小,材料的刚度就越大(沉降结果就 会越小)。
工况阶段[1]:初始地应力场计算
生成网格之后切换到工况阶段[1](使用上方的“工况阶段”工具栏),点击「分析」界面上的“开始分析”按钮得到初始地应力场的计算结果。下图为初始 Z 向有效应力[kPa]。
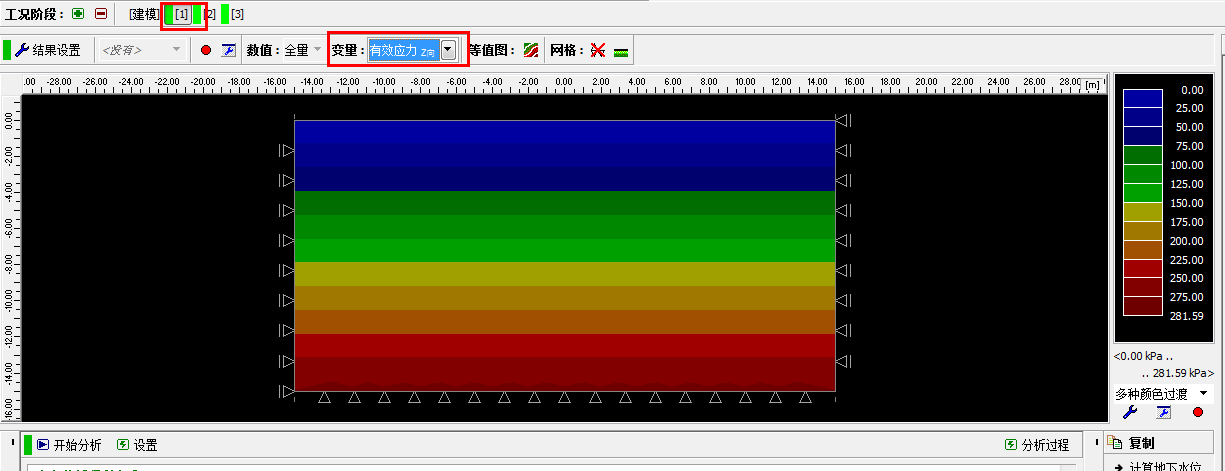
图22.5 工况阶段[1] 分析 – 初始地应力
工况阶段[2]:输入超载
添加工况阶段[2],选择「超载」界面。点击“添加”按钮,弹出“添加超载”对话框,输入超载的各个参数。输入所有参数之后点击“添加”按钮。
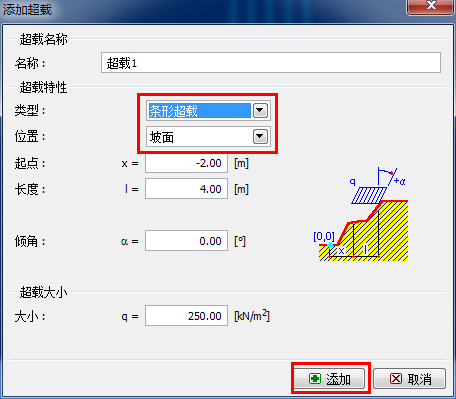
图22.6 添加超载
在此工况阶段,再次分析计算得到结果,观察 Z 向有效应力大小[kPa]。
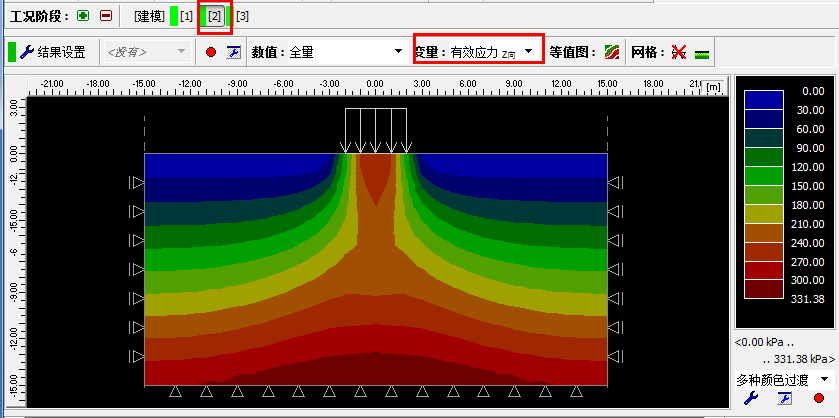
图22.7 工况阶段[2]:分析 – 有效应力 z 向
选择需要显示的结果变量为 Z 向位移[mm],从图中可以看到最大沉降为 107.8mm。
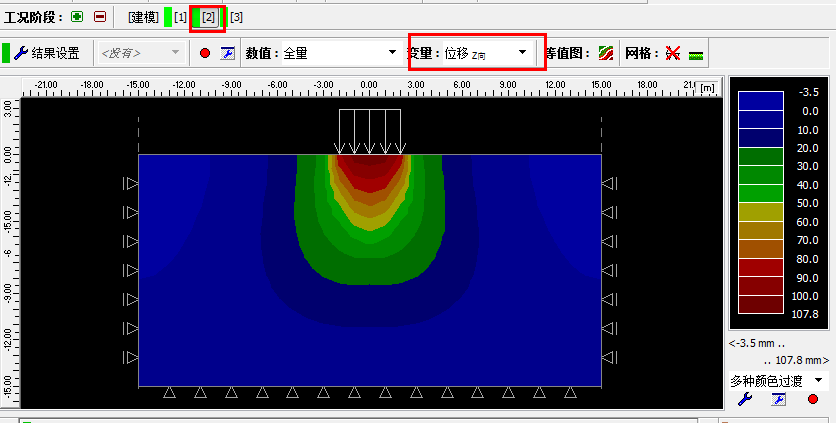
图22.8 工况阶段[2] 分析 – 超载引起的 Z 向位移(沉降)
当有限元分析计算完成后,一个重要的输出参数是等效塑性应变(仅对非线性模型有效)。等效塑性应变区域表示该区域的应力状态已经超出了屈服面,即该区域的岩土体处于塑性变形状态,产生了永久塑性应变。
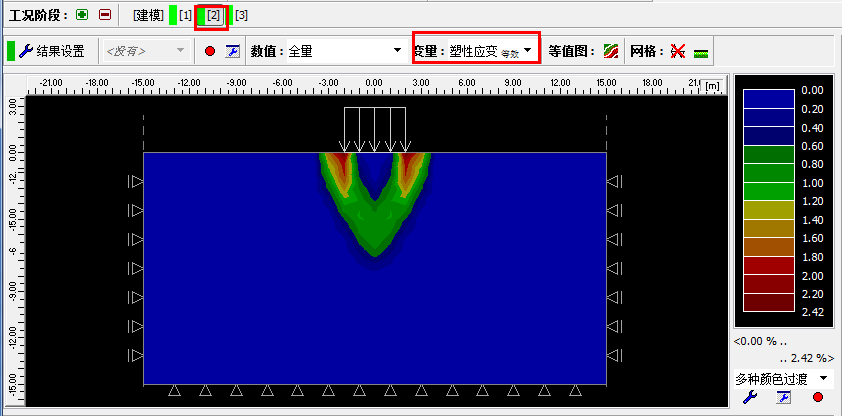
图22.9 工况阶段[2] 分析 – 等效塑性应变
工况阶段[3]:卸载
下一步,添加工况阶段[3]。在此工况阶段中,将超载移除,然后点击“开始分析”按钮得到应力应变结果。当移除超载之后地表最大沉降为 24.1mm(三角形网格)。
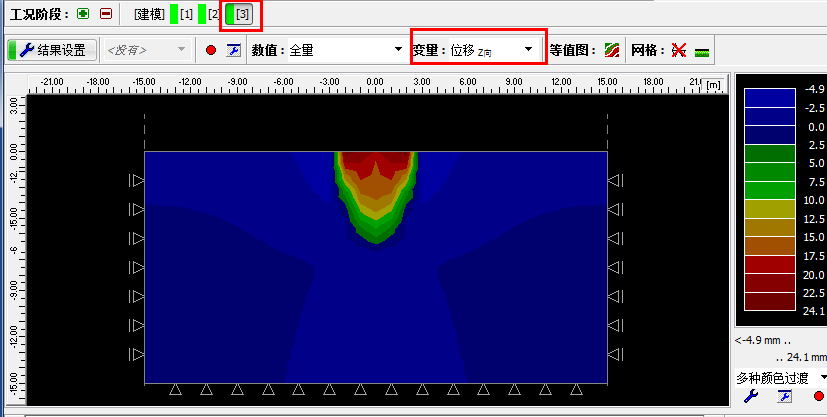
图22.10 工况阶段[3] 分析 – 超载移除后引起的 Z 向位移 dz[mm]
基本的分析计算现在已经完成。接下来,我们会对一些对比分析:采用不同的网格密度(网格边长为1.5m 和 2.0m)和采用不同的本构模型。
22.3结论
下表给出了对同一问题使用不同本构模型、不同网格边长和本算例所得计算结果的对比。除了最后一行数据是采用“GEO5 – 固结沉降分析模块”(基于太沙基固结沉降理论)计算得到的以外,其他数据均由“GEO5 – 有限元模块”计算得到。
表22.2 使用不同本构模型和网格密度计算得到的沉降结果
本构模型/软件 | 网格边长[m] | 工况阶段[2] Z 向位移[mm] | 工况阶段[3] Z 向位移[mm] | 备注 |
| 线弹性模型 | 1.0 | 88.3 | 0 | -- |
| 线弹性模型 | 1.5 | 88.4 | 0 | -- |
| 线弹性模型 | 2.0 | 83.1 | 0 | -- |
| 修正线性弹性模型 | 1.0 | 88.2 | 58.8 | -- |
| 修正线性弹性模型 | 1.5 | 88.3 | 58.9 | -- |
| 修正线性弹性模型 | 2.0 | 83.1 | 55.4 | -- |
| DP | 1.0 | 123.0 | 36.9 | -- |
| DP | 1.5 | 120.7 | 32.5 | -- |
| DP | 2.0 | 120.5 | 42.2 | -- |
| MC | 1.0 | 107.8 | 24.1 | -- |
| MC | 1.5 | 106.9 | 19.7 | -- |
| MC | 2.0 | 106.7 | 28.3 | -- - |
| MCM | 1.0 | 97.5 | 11.1 | -- |
| MCM | 1.5 | 96.3 | 7.8 | -- |
| MCM | 2.0 | 96.0 | 16.4 | -- |
| GEO5 - 沉降模块 | -- | 153.6 | -- | CSN 73 1001 |
注:为了和解析法(太沙基固结沉降理论)的计算结果进行对比,我们还采用“GEO5–沉降模块”对该算例进行了分析。分析设置中选择分析方法为“压缩模量法”,确定变形计算深度的方法为 “结构强度理论”(依据捷克规范 CSN 73 1001)。变形模量取值为 Edef =5.0MPa,结构强度系数 m = 0.2。 若变形计算深度选择应力比法(10%),计算得到的最大沉降为 221.1mm。
从沉降结果的对比中可以得出以下结论:
- 更大的网格密度会导致更大的塑性变形,沉降也会更大。
- DP 模型在该算例中比经典的 MC 模型和 MCM 模型柔度较大。