第二十六章:边坡稳定有限元分析
本例将演示如何使用有限元方法分析边坡稳定性并计算其安全系数。
例题源文件下载地址(v18及以上版本才能打开):http://pan.baidu.com/s/1bpdECj1
26.1任务
首先,分析无超载作用下的边坡稳定性,然后分析在大小为 q=35.0kN/m2的条形超载作用下的边坡稳定性,最后为边坡施加预应力锚杆,并分析其稳定性。边坡的几何尺寸(包括各点的坐标)如下图所示。
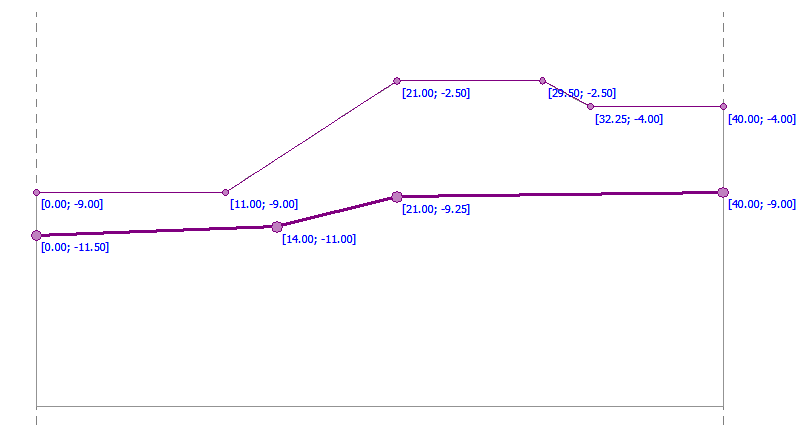
图 26.1 边坡几何尺寸(多段线上各点的坐标)
土层剖面包含两种类型的土,其参数如下:
表 26.1 岩土材料参数列表
| 岩土材料参数/分类 | 岩土材料 1 | 岩土材料 2 |
| 天然重度:γ[kN/m3] | 18 | 20 |
| 弹性模量:E[MPa] | 21 | 300 |
| 泊松比:υ[-] | 0.3 | 0.2 |
| 粘聚力:cef[kPa] | 9 | 120 |
| 内摩擦角:φef[°] | 23 | 38 |
| 剪胀角:ψ[°] | 0 | 0 |
| 饱和重度:γsat[kN/m3] | 20 | 22 |
26.2计算
我们使用“GEO5 岩土工程有限元分析计算模块”(以下简称“有限元模块”)(v18 版)来分析该问题。下面为建模和分析步骤:
- 建模阶段:分析设置和几何建模
- 工况阶段[1]:分析边坡无超载作用时的稳定性
- 工况阶段[2]:分析加入超载后边坡的稳定性
- 工况阶段[3]:分析加入锚杆后边坡的稳定性
- 结论
建模阶段:分析设置和几何建模
在分析设置界面中设置“分析类型”为“边坡稳定分析”,保持其他选项不变。
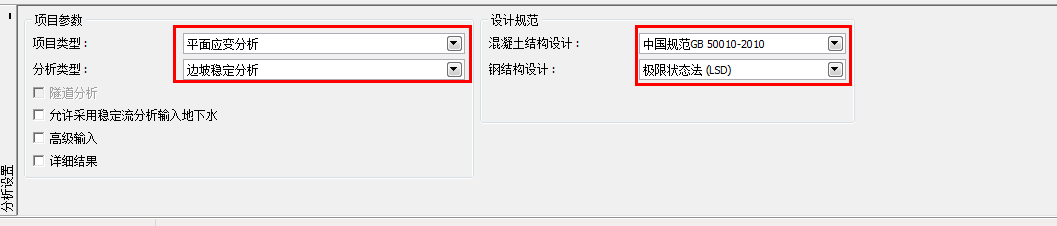
图 26.2 「分析设置」界面
注:选择“边坡稳定分析”时和选择“应力应变分析”时的设置以及建模过程几乎完全一样。在「分析」界面点击“开始分析”按钮即可以分析并计算边坡的安全系数。在“有限元-边坡稳定分析” 模块中,各个工况阶段之间是相互独立的,即当前工况阶段的分析结果不受上一工况阶段分析结果的 影响(详细信息见帮助文档-F1)。
下一步,设置全局坐标范围。设置的坐标范围要足够大,这样才能使得所要分析的区域不受边界 条件的影响。对于该算例,设置全局坐标范围<0m, 40m>,设置底边界距离多段线最低点距离为 10m。
设置各个多段线和土层剖面,其参数如下表所示。
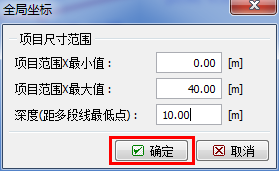
图 26.3 全局坐标对话框
表 26.2 各多段线及其节点的坐标列表
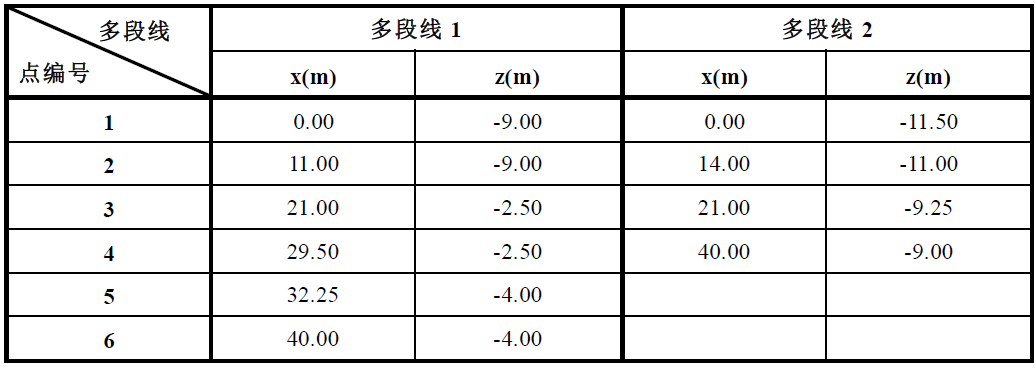
设置各个岩土材料的参数并将其指定到相应的分区。在本算例中,我们选择 Drucker-Prager(DP) 模型(见注)。设置两种岩土材料的剪胀角 ψ 均为 0°,即当材料受到剪力作用时,其体积不发生改变(详细信息见帮助文档-F1)。
注:分析边坡稳定性时,必须选择非线性弹塑性模型作为岩土材料的本构模型,因为在边坡稳定 分析过程中岩土材料会产生塑性应变,且塑性应变的产生是和岩土材料的强度参数 c 和 φ 相关的。
在本算例中,我们选择 Drucker-Prager 作为本构模型,该模型和经典的莫尔-库伦模型相比,允许 产生更多的塑性应变(详细信息见帮助文档-F1)。在本章的最后,将给出不同本构模型下计算得到的 安全系数的对比。
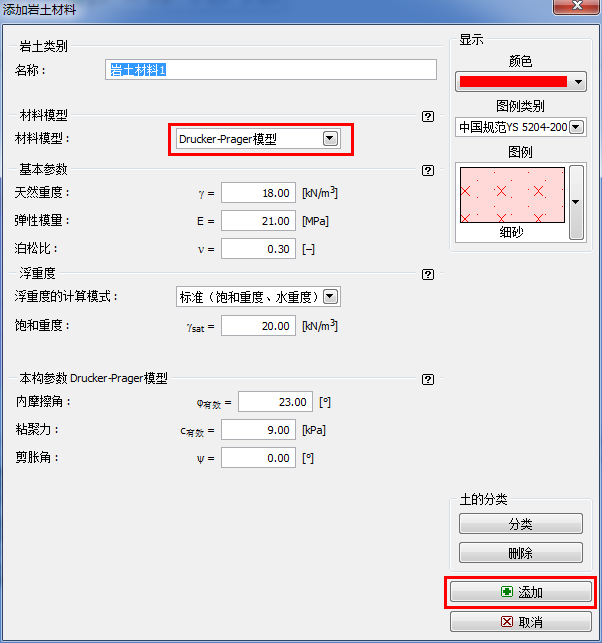
图 26.4 添加岩土材料对话框
下图为指定岩土材料到相应分区之后的剖面。
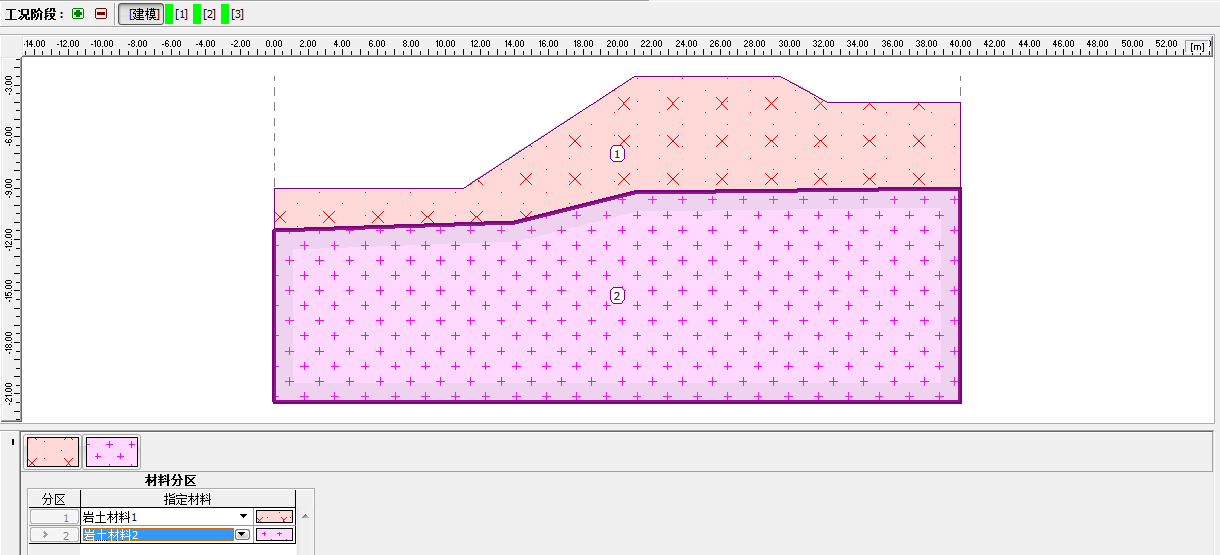
图 26.5 「指定材料」界面
建模阶段的最后一步是生成网格。网格密度对边坡的稳定性分析影响很大,所以必须设置一个足 够大的网格密度。
对本算例,设置网格边长为 1.5m,点击“启动网格生成”按钮生成网格。在本章最后,将给出采用网格边长为 1.0、1.5、2.0m 时计算得到的结果。
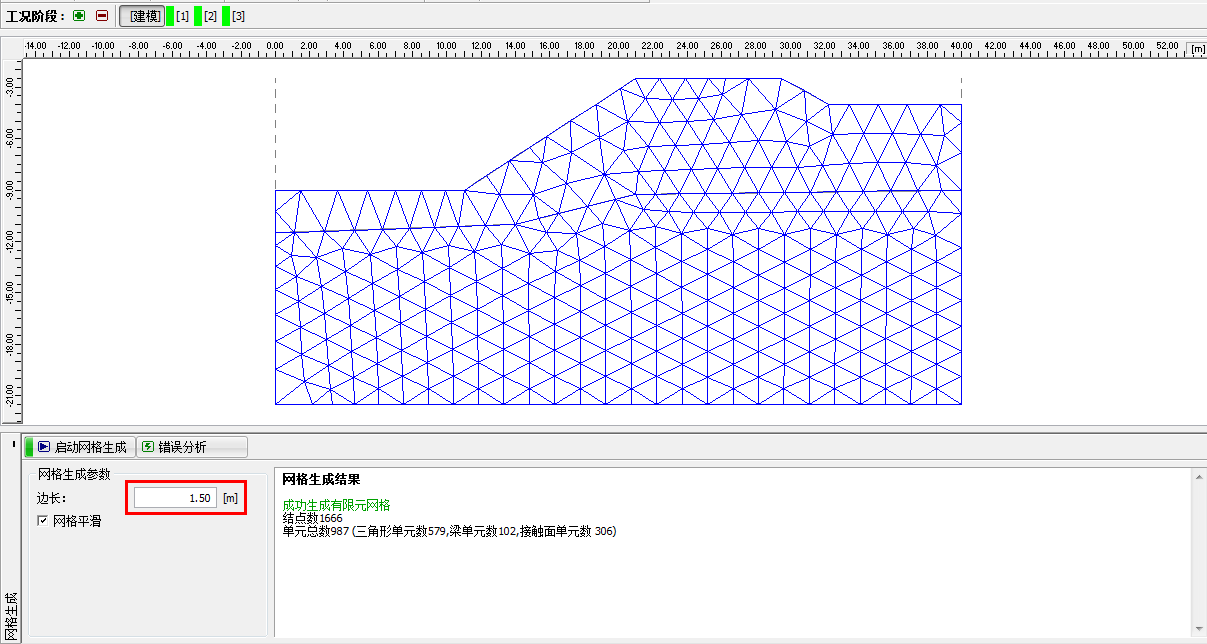
图 26.6 「生成网格」界面–网格边长为 1.5m
工况阶段[1]:分析边坡无超载作用时的稳定性
切换到工况阶段[1],点击“开始分析”按钮进行分析,并保持分析设置类型为“标准”,即默认设置。
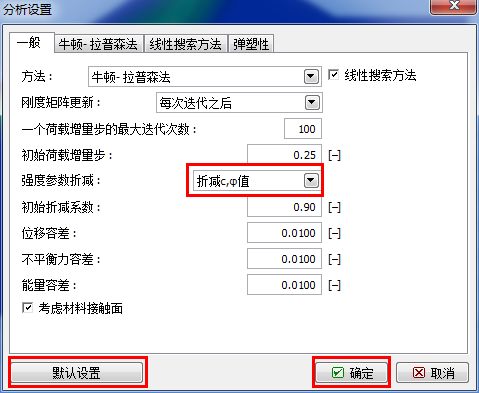
图 26.7 “分析设置”对话框
注:边坡安全系数是通过对岩土材料强度参数 c 和 φ 进行折减得到的(强度折减法)。分析时, 不断折减 c 和 φ 直到边坡达到临界状态(破坏),此时 c 和 φ 的折减系数即为安全系数(详细信息见 帮助文档-F1)。因此,程序通过下式得到边坡的安全系数:
FS=tanφs/tanφp
其中:φs – 真实内摩擦角
φp– 边坡失稳时的内摩擦角
在边坡稳定性分析中,非常重要的两个计算结果为位移矢量图和等效塑性应变 εeq.,pl图。等效塑 性应变区域即为边坡的潜在破坏区域(见下图)。
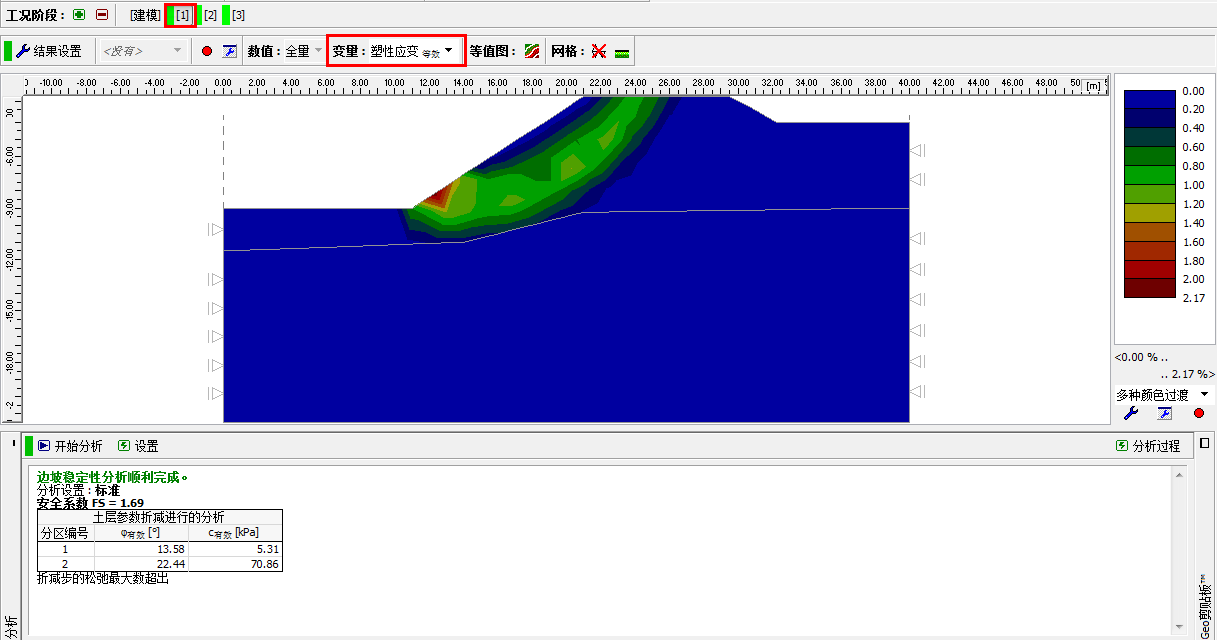
图 26.8 「分析」界面–工况阶段[1](等效塑性应变 εeq.,pl)
注:“有限元-边坡稳定分析”模块的分析结果中包括位移等值图(Z 向和 X 向)和应变等值图(总应变、等效塑性应变)。软件得到的计算结果是折减参数之后的情况,因此该结果和实际的情况是不同,该结果表示的是边坡失稳时的情况(详细信息见帮助文档-F1)。
工况阶段[2]:分析加入超载后边坡的稳定性
添加工况阶段[2],在「超载」界面中定义如下图所示类型的超载。
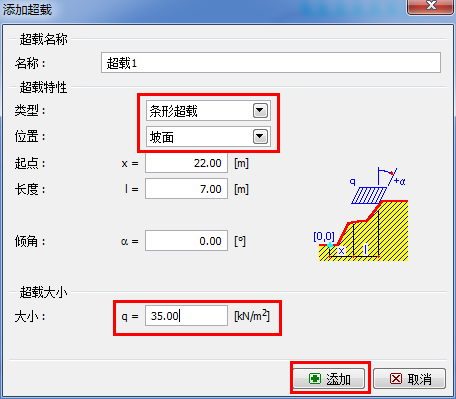
图 26.9 “添加超载”对话框–工况阶段[2]
点击“开始分析”按钮得到分析结果,观察等效塑性应变等值图。
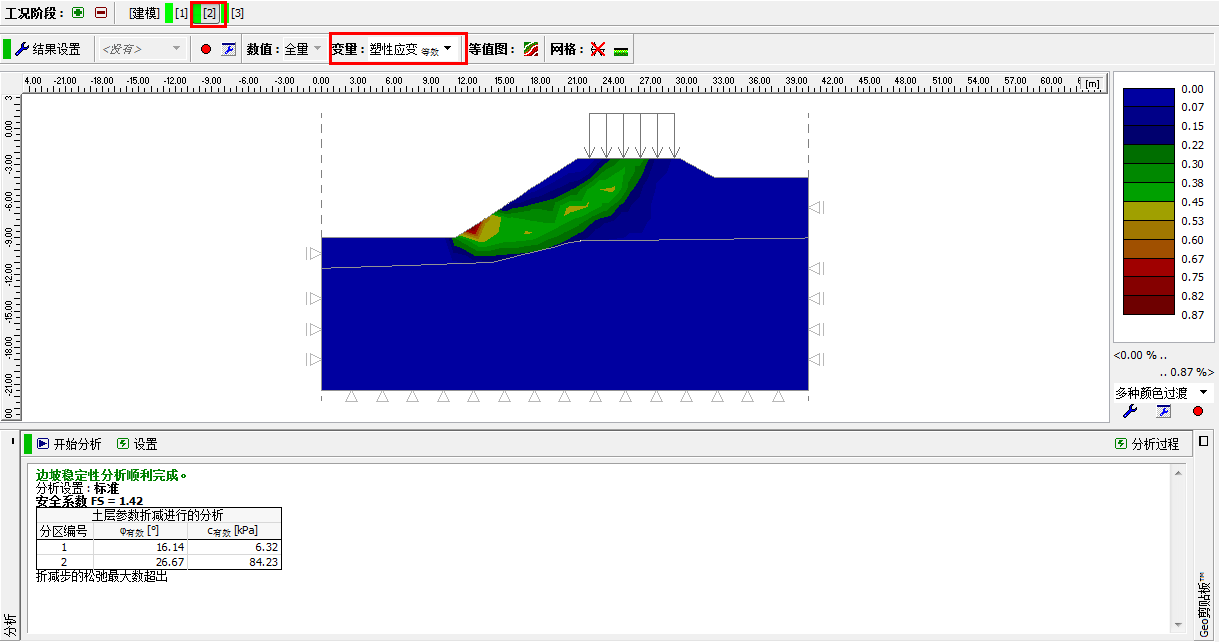
图 26.10 「分析」界面–工况阶段[2](等效塑性应变 εeq.,pl)
工况阶段[3]:分析加入锚杆后边坡的稳定性
添加工况阶段[3],在「锚杆」界面中点击“添加”按钮,弹出添加锚杆对话框,输入如下所示的锚杆参数,锚杆预应力为 F=50kN。
- 锚杆长度: l=16m
- 倾角: α=17°
- 锚杆水平间距:b=1m
- 锚杆直径:d=20mm
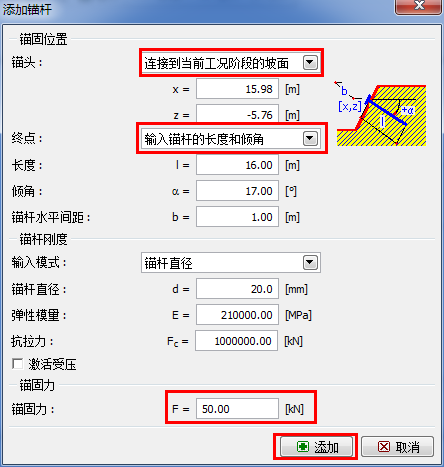
图 26.11 添加锚杆对话框–工况阶段[3]
注:在进行边坡稳定性分析时,预应力锚杆中的预应力采用作用在锚头处的等效集中压力代替。集中压力作用点处的岩土材料可能会发生塑性变形。由于等效塑性应变的位置即为潜在滑动面的位置, 因此,用户应当对得到的塑性应变分布进行认真分析。如果得到的锚头附近塑性应变对边坡稳定性起 着决定性作用,那么这时用户必须对初始输入参数进行一些修改(详细信息见帮助文档-F1)。
其他参数保持不变,点击“开始分析”按钮分析得到结果,并观察得到的等效塑性应变等值图(和 前一工况阶段类似)。
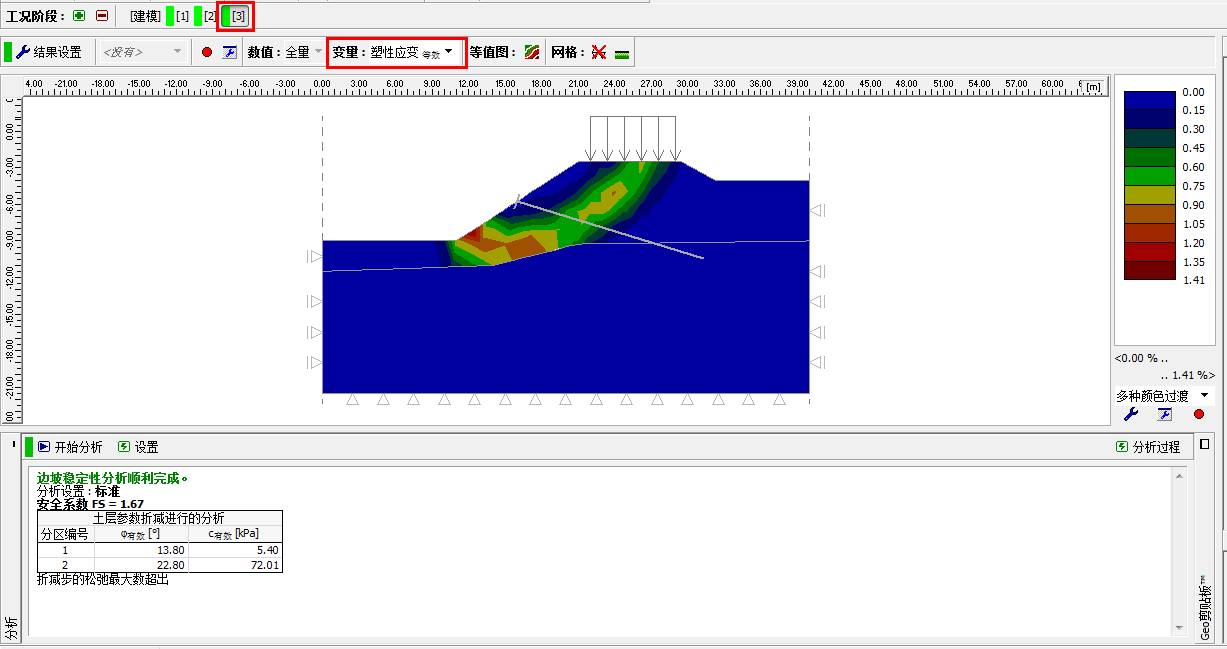
图 26.12 「分析」界面–工况阶段[3](等效塑性应变 εeq.,pl)
现在,将分析得到的安全系数记录到一个表格中,然后采用其他的本构模型(莫尔-库伦模型(MC), 修正莫尔-库伦模型(MCM))再次分析该问题。
注:检验计算得到的滑面形状(等效塑性应变带)是非常重要的,因为,在某些情况下,局部的 失稳可能发生在我们认为不会发生失稳的区域(详细信息见帮助文档-F1)。当采用 DP 模型并设置网 格边长为 1m 时,将会得到下图中的结果。从图中可以看出,锚头附近的土体出现了局部破坏,但是 边坡本身却没有发生破坏,这时得到的安全系数并不是边坡的安全系数。如果这种情况发生,可以对 于模型的参数进行一定的修改,例如:
- 增大网格边长;
- 将锚头附近岩土材料的强度参数提高(具有更高的 c 和 φ),或采用弹性模型;
- 在锚杆锚头下设置一个梁单元(这样可以让预应力能均匀的传递到岩土材料中)。
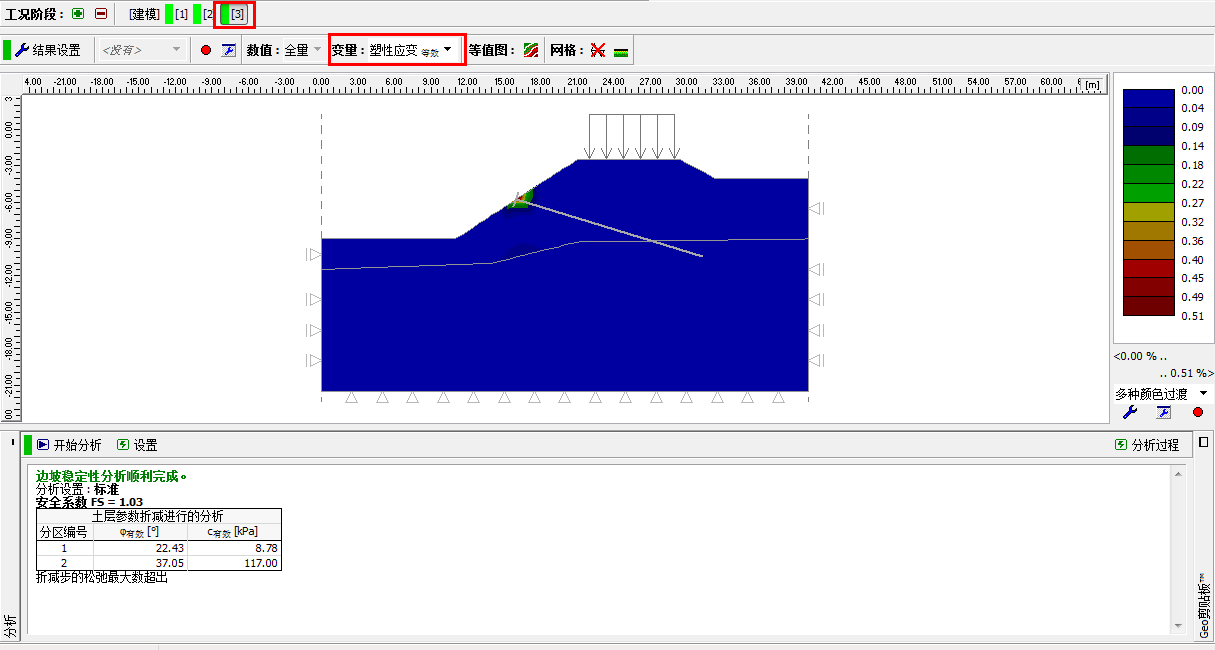
图 26.13 「分析」界面–工况阶段[3](锚头附近产生局部塑性应变,DP 模型,网格边长 1m)
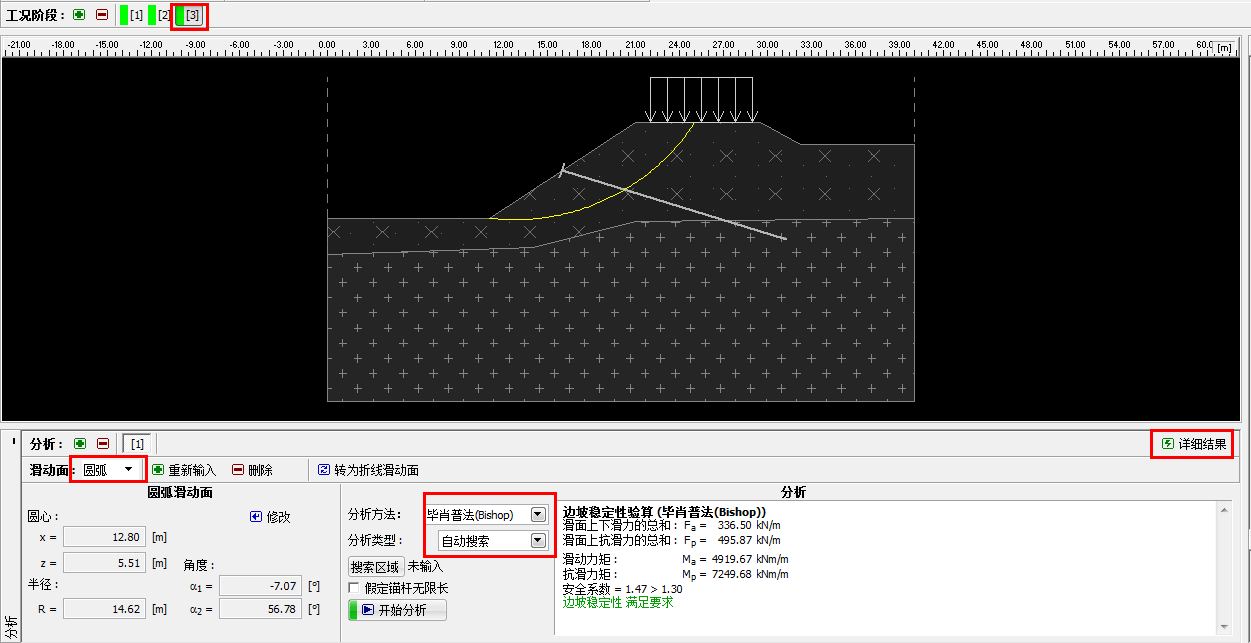
图 26.14 「分析」界面–工况阶段[3](使用极限平衡法中的 Bishop 法分析得到的圆弧滑面)
26.3结论
下表列出的是各个工况阶段采用不同的非线性本构模型和网格密度得到的边坡安全系数。为了对 比,我们还列出了“GEO5-土质边坡稳定分析”模块中采用 Bishop 法和 Spencer 法得到的安全系数。
表 26.3 使用不同本构模型和方法得到的边坡安全系数
| 本构模型 | 网格边长[m] | 工况阶段[1]FS | 工况阶段[2]FS | 工况阶段[3]FS | 注 | |
| DP | 1.0 | 1.67 | 1.44 | 1.03 | 锚头附近区域发生局部塑性应变 | |
| DP | 1.5 | 1.69 | 1.42 | 1.67 | ||
| DP | 2.0 | 1.74 | 1.48 | 1.69 | ||
| MC | 1.0 | 1.56 | 1.35 | 0.90 | 锚头附近区域发生局部塑性应变 | |
| MC | 1.5 | 1.58 | 1.35 | 1.56 | ||
| MC | 2.0 | 1.60 | 1.41 | 1.56 | ||
| MCM | 1.0 | 1.78 | 1.56 | 1.14 | 锚头附近区域发生局部塑性应变 | |
| MCM | 1.5 | 1,81 | 1.54 | 1.78 | ||
| MCM | 2.0 | 1.85 | 1.60 | 1.81 | ||
BISHOP极限平衡法 | - | 1.51 | 1.33 | 1.47 | 见下文 | |
SPENCER极限平衡法 | - | 1.51 | 1.32 | 1.52 | 见下文 |
注:采用极限平衡法时,在“土质边坡稳定分析”模块中选择“标准-安全系数法”作为分析设 置,并分别使用 Bishop 法和 Spencer 法搜索得到最危险圆弧滑面(不限制搜索区域)。
从上面的分析结果可以得出如下结论:
- 对某些重点区域的网格进行局部加密会得到更为精确的结果,但是另一方面,会使得各个工况阶段的分析时间增加。
- 边坡稳定分析中必须使用允许发生塑性变形的非线性弹塑性模型。
- 最大等效塑性应变 εeq.,pl 发生的区域为潜在破坏区域。
- DP 本构模型得到的安全系数比 MC 模型得到的稍大,即 DP 模型允许更大的塑性应变。