第三十六章：有限元强度折减法——不折减强度区

36.1  简介

　　采用有限元强度折减方法分析岩土体稳定性时，通过逐步折减岩土体的抗剪 强度参数来找到岩土体承载力与荷载之间的极限平衡状态。极限平衡状态的破坏 通过非线性数值分析的不收敛来体现。“不折减强度区”功能允许在进行强度折 减分析时，选定某些区域的岩土体抗剪强度参数不被折减。

36.2  何时需创建不折减强度区

　　当遇到以下两种情况时可以考虑不折减剪强度参数：

　　（4）计算整体稳定性安全系数的过程中出现了局部塑性区，并可能导致计算不收敛，从而只能得到局部稳定性安全系数。

　　（5）由于边界条件和计算模型尺寸的影响，由整体滑动引起的局部塑性区 在整个模型范围内产生了不合理的发展。

36.3  何种材料模型可以应用不折减强度区

　　不折减强度区仅可用于可进行有限元强度折减分析的材料本构模型，因此， 以下几种材料模型可应用不折减强度区：

　　Mohr-Coulomb 模型

　　修正的 Mohr-Coulomb 模型

　　Drucker-Prager 模型

36.4  不折减强度区的岩土材料参数

　　不折减强度区内的网格单元在稳定性分析中始终保持决定其刚度大小的和 抗剪强度的参数（黏聚力和内摩擦角）不变。不过，该区域的网格仍然可能发生塑性变形。

36.5  采用不折减强度区的注意点

　　当使用“不折减强度区”功能时，应注意该区域内的岩土材料抗剪强度参数不会改变（折减）。因此，不折减强度区不能对整体滑动滑面可能经过的区域产生影响，否则会影响计算得到的整体稳定性安全系数。

36.6  如何创建不折减强度区 

注：当需要对“应力应变”分析的某一工况阶段进行稳定性分析时（边坡稳定分 析 – 有限元强度折减法），可以直接在当前工况阶段启动“有限元边坡稳定分 析”模块。

　　当选择分析类型为“边坡稳定分析”时，可以在不同工况阶段添加不折减强 度区。可直接在绘图区鼠标点击输入多边形的顶点来创建不折减强度区。全部或 部分落入不折减强度区的单元都将被高亮标示，这些单元都属于不折减强度参数 的单元。

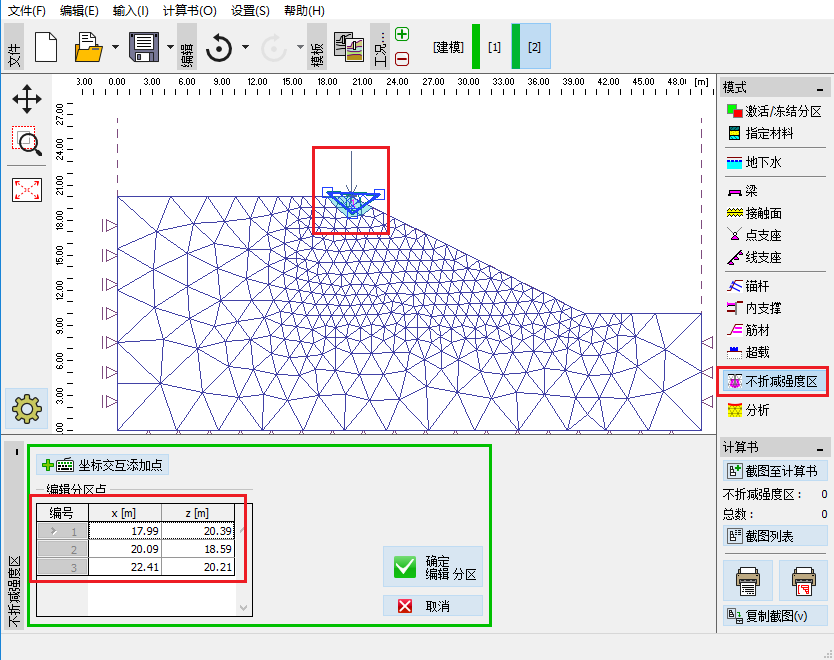
图 36.1  创建不折减强度区

注：在创建不折减强度区的时候可通过如下图 36.2 所示操作来显示有限元网格， 这将更有利于不折减强度区的划分。

　　不折减强度区创建后在后续工况阶段依然保持有效，但是可以在后续工况阶 段中删除。若删除不折减强度区，那么相应区域内岩土体的强度参数将恢复可以被折减状态。

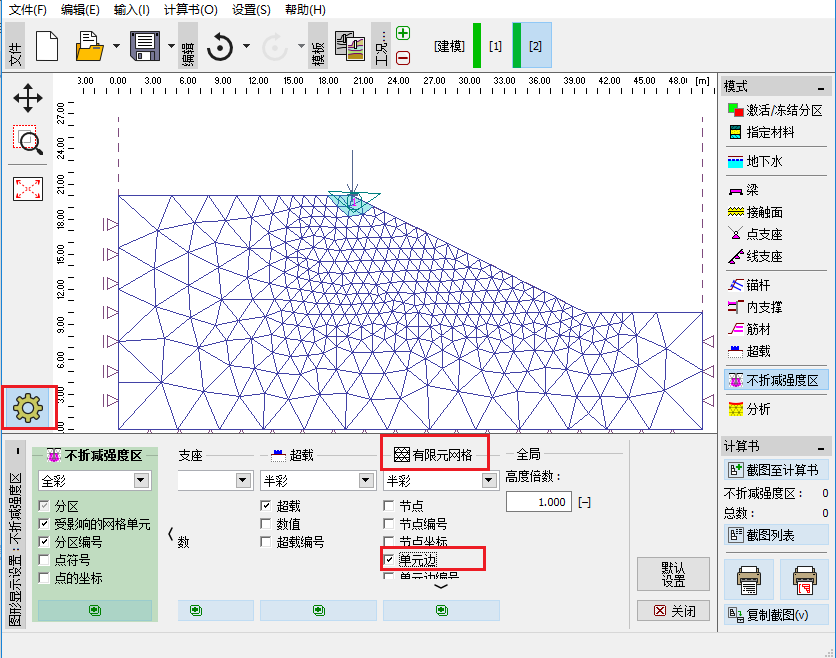
图 36.2  设置显示有限元网格

36.7 不折减强度区应用实例

　　这里通过分析顶部作用有线荷载的边坡的稳定性来说明不折减强度区域的 使用。几何尺寸、岩土材料、工况阶段均已在例题源文件中给出。

　　如下图 36.3 为失稳后等效塑性应变的分布图。从图中可以看出，除了在施 加线荷载的地方有局部塑性区的发展，分析结果还表明模型中心区域也产生了非 常不合理的大范围的等效塑性应变，其发展趋势和模型的尺寸以及边界条件有 关。当前得到的等效塑性应变分布并不是整体滑动面的位置，因此，所得到的安 全系数 1.14 也是不合理的。

　　添加工况阶段 2，在线荷载作用位置创建一小块不折减强度区，如图 36.4所示。

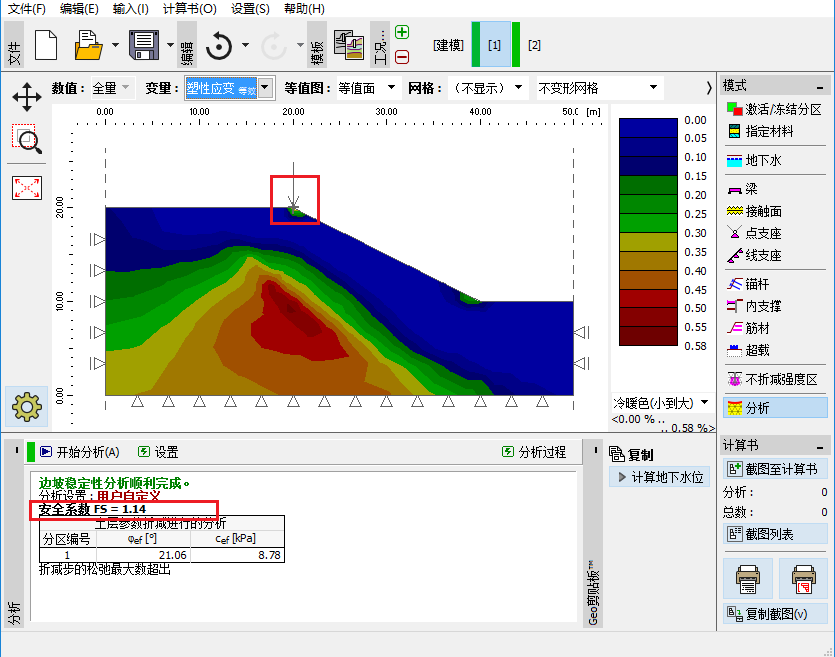
图 36.3  不合理的等效塑性应变分布

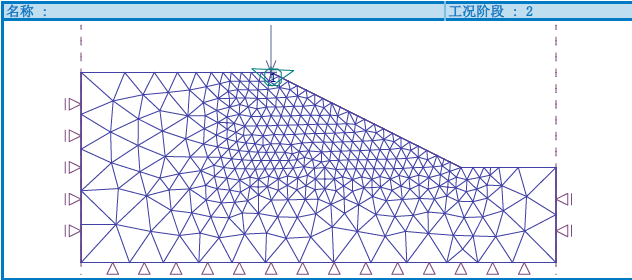
图 36.4  创建不折减强度区

　　创建了不折减强度区以后的边坡稳定性分析（强度折减法）结果如图 36.5 所示。从图中可以看出，整体滑动面的位置和形状均相对更合理。由于边界条件 引起的中央区域的塑性应变仍然存在，但该区域的塑性应变大小与滑动面位置的 塑性应变相比要小得多，并且对边坡失稳（不收敛）也没有太大的影响。因此， 计算得到的安全系数 1.60 是合理的。

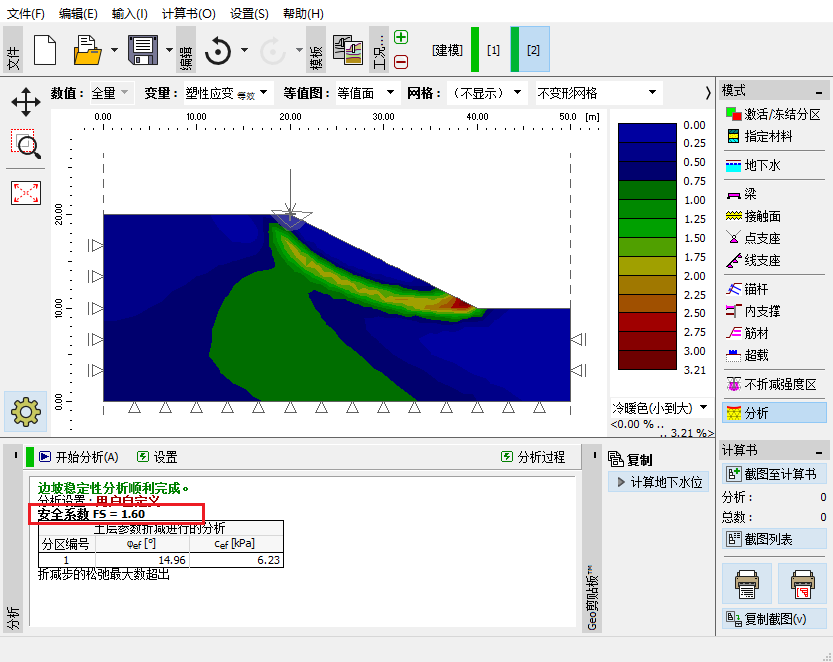
图 36.5  等效塑性应变的分布表明了整体滑动面的位置

36.8  结论

　　在边坡稳定性分析（有限元强度折减法）中使用“不折减强度区”功能可以 在部分区域内保持岩土体的抗剪强度参数在分析过程中不被折减。此功能只能用 在由于其他原因而非全局失稳所造成的分析不收敛问题上。