固结沉降

固结沉降的最终沉降量s通常被作为实际沉降量使用。通常采用下面两种假设中的一种进行计算：

• 线性弹性变形
• 非线性弹性变形

线性弹性变形

应力应变的线性关系满足Hook定律：

只有当受力变形的岩土体可以在水平方向发生变形时，弹性杨氏弹性模量E才是可用的，但是，这只适合于小型的扩展基础。当荷载作用于一个更大的区域时，除了荷载作用范围的边缘地带，岩土体并不能向两侧发生压缩变形。这时岩土体只能发生竖向变形（一维变形），可采用大于杨氏弹性模量E的侧限压缩模量E_oed。

岩土体的沉降量s由岩土体的应变ε乘上岩土体的厚度（高度）H_o得到：

按照分层总和法的计算思想，将各层的沉降量相加，得到总的沉降量：

非线性弹性变形

大部分岩土体的应力应变关系都是非线性的，并且还受到加载历史的影响。在计算细粒土（粉土、粘土）的沉降时，应力应变关系的非线性性尤其不能忽略。因此，基于弹杨氏性模量的线性弹性变形沉降计算方法并不能适用于大部分情况，即使是使用基于压缩模量的方法也不能得到某些超固结土沉降的合理预测值。非线性弹性模型使用的参数主要有孔隙比，以及岩土体的竖向变形相关参数，例如压缩常数、压缩指数等。

下图说明了利用孔隙比e计算厚H_o宽B = 1 m的可压缩饱和土沉降量的步骤：

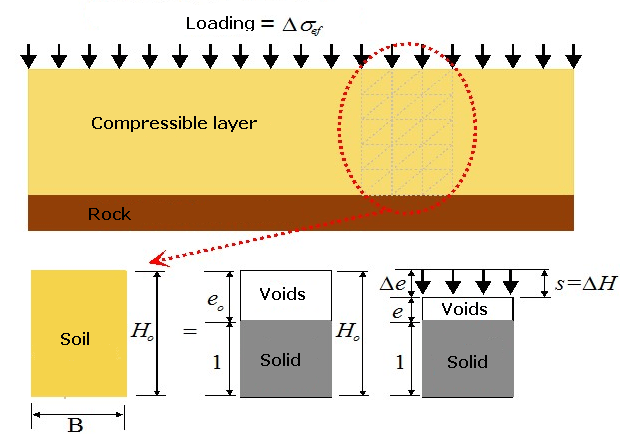沉降计算图

由于土体是三相介质（包含土颗粒、孔隙中的水和空气），可采用土颗粒体积V_s来描述固相（岩石颗粒和矿物颗粒），采用孔隙比e来描述气相和液相。

岩土体受到其上方均布荷载q的作用时，其应力将发生变化并引起土体的竖向变形ΔH，孔隙体积V_p和孔隙比e将减小（从初始孔隙比e_o变为一个新的孔隙比e）。岩土体的竖向应变ε等于ΔH比上岩土体初始高度H_o，同时也可以用孔隙比e来表示：

对上面的方程进行一定的变换，得到计算岩土体沉降量的方程如下：