折线滑动面

折线滑面的边坡稳定性问题求解思路是确定作用在滑面上方土体的受力极限状态。为了引入这些作用力，通过分割面将滑面上的土体划分为若干条块。一般而言，分割面都假设为竖直平面，但这并不是必要条件，比如 Sarma 法则可以考虑倾斜面。

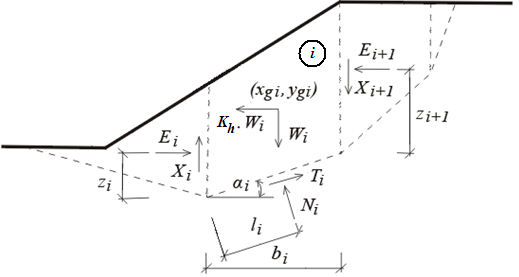条块受力平衡示意图

上图显示的是各条块上的作用力。如果滑面以上的土体被划分为若干条块，则计算中的未知变量有：n 个作用在各条块底部的法向力 N_i 和相应的 n 个剪切力 T_i；n-1 个条块间作用的法向力 E_i 和相应的 n-1 个剪切力 X_i；n-1 个表示 E_i 作用点的 z_i 值；n 个表示 N_i 作用点的 l_i 值和一个安全系数值 SF。在某些方法中，作用力 X_i 可以用条块间作用力 E_i 的倾角代替。

联立下列方程可以求解平衡问题：对于各条块可以写出 n 个水平向和 n 个竖直向的受力平衡方程，n 个力矩平衡方程以及根据Mohr-Coulomb理论得到的 n 个 N_i 与 T_i 的关系式。总共得到 4n 个方程式，而其中的未知量有 6n-2 个。这表明 2n-2 的变量值必须事先确定。各种计算方法之间的不同之处就在于这2n-2个变量的选取。

大多数情况下事先确定的变量是条块间作用力的作用点或其施加方向的倾角值。在分析中使用迭代方法求解平衡问题，计算时选择的初始值必须能同时满足平衡和运动学容许性条件。

对于折线形滑动面，软件中有以下几种方法可供选择：

• Sarma法
• Spencer法
• Janbu法
• Morgenstern-Price法
• Shahunyants法
• 不平衡推力法

折线形滑动面的自动搜索过程将搜索出最危险的滑面（安全系数最小的滑面）。