求解过程
求解过程
岩石边坡稳定性分析中折线滑动的计算原理如下图所示。
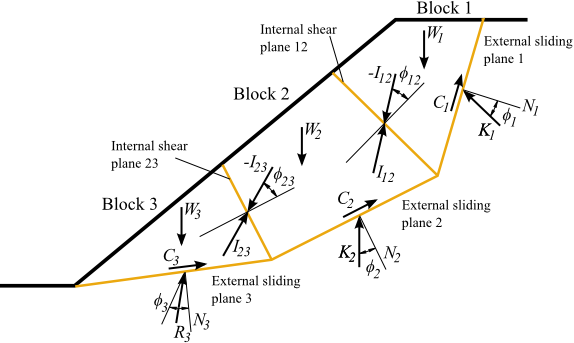折线滑动中作用在各个岩块上的力
假设向量D1为作用在岩块1上的所有扰动力的合力：
其中： | W1 | - | 岩块自重向量，作用方向竖直向下 |
E1 | - | 地震作用力向量 | |
U1 | - | 地下水产生的扬压力向量，作用方向垂直于滑面 | |
V1 | - | 张裂缝中作用的水压力向量 |
假设N1为滑面1的单位法向向量，ϕ1为滑面1的内摩擦角。当滑块1的合力落于滑面1的摩擦锥之外时，滑块1就可能处于不稳定状态，即：
其中： | R1 | - | 作用在滑块1上的扰动力和抗力的合力的单位方向向量 |
N1 | - | 滑面1的单位法向向量（向上） | |
ϕm1 | - | 已激发内摩擦角（mobolized angle of internal friction） |
如果岩块1不稳定，那么岩块1将对下一岩块2产生作用力。此作用力用向量I12表示：
其中： | K1 | - | 滑块1的反力，极限平衡状态时作用方向与滑面法向的夹角为ϕ1，如上图所示 |
滑块2的分析和滑块1类似，唯一的区别在于滑块2中需要考虑滑块1对滑块2的作用力I12。合力R2由下式表示：
其中： | D2 | - | 作用在滑块2上的所有扰动力的合力（向量） |
Cm2 | - | 已激发的剪力（mobilised shear force）（向量） | |
B2 | - | 作用在滑块2上的由锚杆等支护结构引起的外力合力（向量） | |
I12 | - | 滑块1作用在滑块2上的力（向量） |
因此，从最上方的岩块1开始，依次向下，对每一个岩块均进行相同的稳定性分析，直到最下方的岩块n。如果最下方岩块的合力落于相应滑面的摩擦锥内，则认为所有的岩块都是稳定的，即边坡是稳定的。以上图为例，其中最下方的岩块编号为3，当满足下面的条件时，稳定的岩块可以为不稳定的岩土提供足够的抗滑力，整个边坡系统是稳定的：
其中： | R3 | - | 作用在滑块3上的扰动力和抗力的合力的单位方向向量 |
N3 | - | 滑面3的单位法向向量（向上） | |
ϕm3 | - | 已激发内摩擦角（mobolized angle of internal friction） |
