非线性模型

基本的非线性模型可以进一步分为两种类型。

第一类模型基于Mohr-Coulomb（莫尔-库伦）破坏准则。Drucker-Prager模型，Mohr-Coulomb弹塑性模型，修正Mohr-Coulomb弹塑性模型都属于这一类。这类模型可以模拟材料的硬化和软化，且其共同特点是当沿着静水压力轴（σ₁=σ₂=σ₃）对材料施加压力时，材料只发生弹性变形。从下方屈服面在偏平面和子午面上的投影图可以清楚地看出这一点。这里展示了一个所选模型分析结果的实例。

第二类模型的代表模型是修正Cam-clay模型（修正剑桥模型），广义Cam-clay模型（广义剑桥模型）和亚塑性模型，这类模型的理论基础是临界状态土力学。

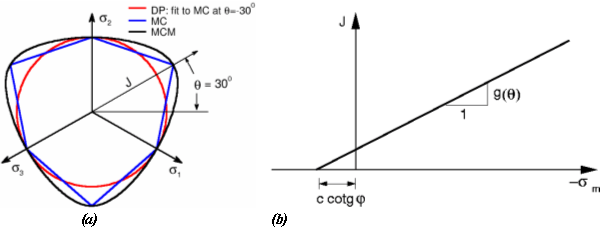屈服面在偏应力平面（a）和子午面（b）上的投影

采用非线性模型可以得到岩土材料的非线性应力应变行为。

这些模型描述了岩土材料永久变形（塑性变形）的过程。塑性变形的起始点由屈服面控制，这个屈服面可以是恒定的（理想弹塑性材料），也可以由所处的应力状态决定（材料的硬化/软化）。

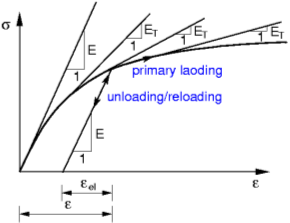非线性模型的应力-应变关系图

不同于修正线弹性模型，非线性模型只需要指定弹性模量。材料刚度的降低是因为产生了塑性变形和应力的重新分布，因此，材料刚度的瞬时切线模量是当前应力状态的函数，随应力状态的变化而变化，图中的瞬时切线模量E_T所示。

除了在“线弹性模型”章节中描述的基本材料参数，非线性模型还需要一些用于定义屈服面的岩土材料强度参数。参考第一类材料模型，有限元分析需要下列参数：

内摩擦角和粘聚力决定了塑性变形的起始点。剪胀角控制着塑性体积应变的发展（剪胀）。