亚塑性模型

亚塑性模型适用于较软的细粒土。和很多其他模型类似，该模型也属于标准的现象学模型家族。在分析岩土体应力应变方面，它属于临界状态模型（修正剑桥模型，广义剑桥模型）。但是，亚塑性模型可以同时反映岩土体在加载和卸荷时的非线性应力应变行为。和其他基于弹塑性理论的模型相比较，亚塑性模型可以只计算总应变，因此，亚塑性模型中并不区分弹性应变和塑性应变。在其他模型中，潜在滑动面的类型和位置可以通过绘制等效塑性偏应变来表示，但是，在亚塑性模型中，潜在滑动面可以通过机动摩擦角的分布来表示。

描述岩土体的应力应变行为时，亚塑性模型可以根据岩土体的压缩情况以及剪切时剪胀或剪缩的情况区分加卸载的不同，同时，岩土体当前刚度仅由加载方向和当前孔隙度确定。和修正剑桥模型不同，亚塑性模型不考虑岩土体中的拉应力，如图1a所示。

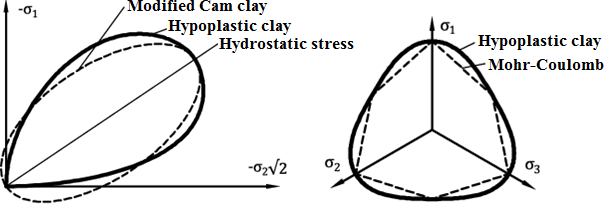图1：亚塑性模型的状态边界 – (a)与子午面上修正剑桥模型屈服面的对比，(b)与偏应力平面上摩尔-库伦模型屈服面的对比

在亚塑性模型中，屈服面被所谓的状态边界面代替。它在偏应力平面上的投影和屈服面很像，如图1b。流动法则采用的是非流动法则，因此刚度矩阵式非对称的（例如，和内摩擦角φ以及剪胀角ψ不同的摩尔-库伦模型相比较）。关于该模型的具体方程可以参考文献[1]。

模型参数

亚塑性模型最基本的变量为以下五个材料参数：

• 体积恒定时的内摩擦角（临界内摩擦角）φ_cv
• 回弹曲线斜率κ*
• 正常固结曲线斜率（NCL）λ*
• 正常固结曲线原点N
• 体积模量和剪切模量的比值r

参数κ*，λ*和N定义了一个在双对数坐标中的双线性各向等压固结曲线图，如图2a。假如已知双线性修正剑桥模型的参数（半对数坐标，如图2b），可以通过这些参数反算出亚塑性模型的参数。双线性修正剑桥模型的参数为：

• 回弹曲线斜率κ （半对数坐标）
• 正常固结曲线斜率λ （半对数坐标）
• 1kPa压力作用下竖向等压固结时的孔隙比e_max

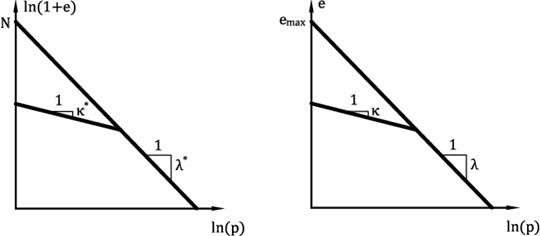图2：等压固结双线性曲线图 – (a)亚塑性模型，(b)修正剑桥模型

临界内摩擦角φ_cv

• 对原状土和重塑土都具有相同的值
• 可以通过在标准三轴试验中对重塑土施加不同的围压来测得
• 可以采用排水试验，也可以采用不排水试验（更快）
• 取值范围通常为18° – 35°

正常固结曲线斜率λ*

• 通过侧限压缩固结加载曲线或等压固结加载曲线得到，如图3
• 对于硬粘土，最好采用重塑土试样来进行试验
• 取值范围通常为0.04 – 0.15

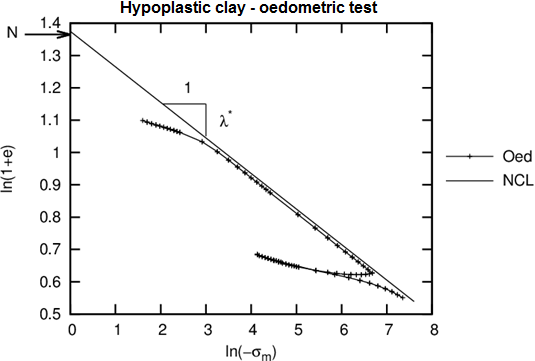图3：采用亚塑性模型模拟侧限压缩固结试验

回弹曲线斜率κ*

• 确定该参数的方法和确定参数λ*类似，可以通过侧限压缩固结卸载曲线或等压固结卸载曲线来得到，如图3
• k的取值范围统称为0.01 – 0.02
• λ/κ的比值应大于4.0

正常固结曲线原点N

• 通过侧限压缩固结加载曲线或等压固结加载曲线得到
• 当想要确定正常固结曲线和竖向坐标轴的交点时，应当采用原状土试样来进行试验。如果仅仅只是确定正常固结曲线的斜率，可以采用重塑土试样来进行试验，如图3
• 取值范围通常为0.8 – 1.6

体积模量和剪切模量的比值r

• 该参数的物理意义由表达式r = K_i/G_i表示
• K_i是等向压缩正常固结曲线的切线体积模量
• G_i是相同应力状态下，不排水剪切试验的切线剪切模量
• 参数r可以通过三轴剪切试验得到
• 取值范围通常为0.05 – 0.7

设置岩土体初始状态

亚塑性模型中岩土体的当前状态是和由孔隙比表示的当前岩土体压缩状态相关的。建模时可以直接输入初始孔隙比或当前孔隙比，也可以由软件通过超固结比OCR计算得到。对于第一种情况，输入的初始孔隙比e₀对应于给定深度处卸载土样的孔隙比，如图4a。对于第二种情况，输入的当前孔隙比e_curr对应于当前受压土样的孔隙比。对于最后一种情况，直接输入超固结比OCR的值即可。该参数是初始平均应力和正常固结曲线上平均应力的比值，如图4b。

当采用侧压力系数K_o法进行初始地应力平衡时，第二工况阶段开始时的初始应力状态即为根据K_o的大小指定的应力状态。如果采用自重应力法进行初始地应力平衡（在第一工况阶段已经采用了亚塑性模型），则假设初始应力为pin = 1 kPa，保持e_curr = e₀，作用荷载为土体自重。假如某种不同的岩土材料（例如，在第一工况阶段中指定材料模型为线弹性材料）被亚塑性模型替换了（例如在第二工况阶段），那么亚塑性模型的初始应力状态将直接继承前一工况阶段结束时的应力状态。可以注意到，如果第一工况阶段采用线弹性模型，那么得到的应力状态和采用侧压力系数K_o法计算得到的应力状态相同，且K_o的取值如下式所示（ν为泊松比）。

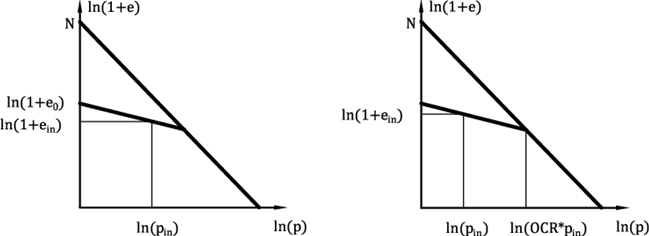图4：孔隙比初始化 – (a)直接输入初始孔隙比，(b)由超固结比OCR初始化

从图5中可以清楚的看出，对于正常固结土，即超固结比OCR = 1.0的各向等压固结，其K_o = 1.0。如果土体处于非零偏应力状态，那么对于正常固结土，其超固结比OCR大于1.0。K_o的准确值和岩土体参数及其应力路径有关。图5为不同类型粘土的最小超固结比和K_o的关系图。表1为相应的试验数据，表2为试验所用粘土的材料参数。

对于正常固结土，OCR = 1.0，若此时K_o不等于1.0，那么此时计算出来的应力状态是不对的，同时在计算时也可能会导致不收敛。

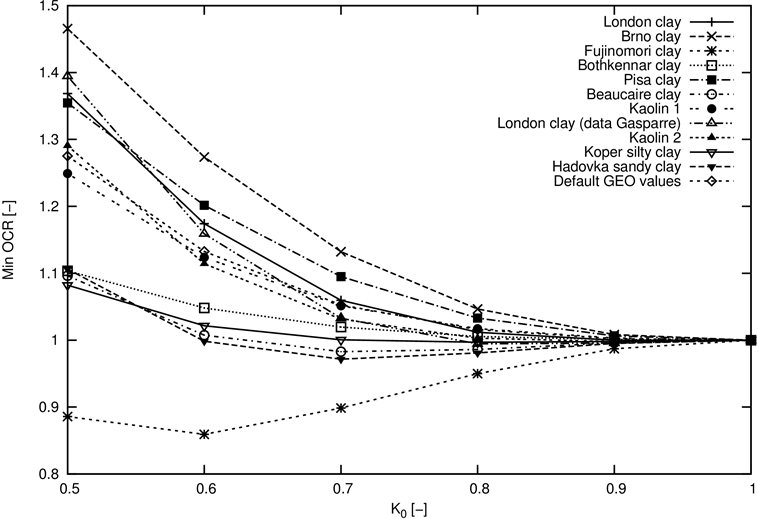图5：超固结比OCR与静止土压力系数Ko的关系曲线

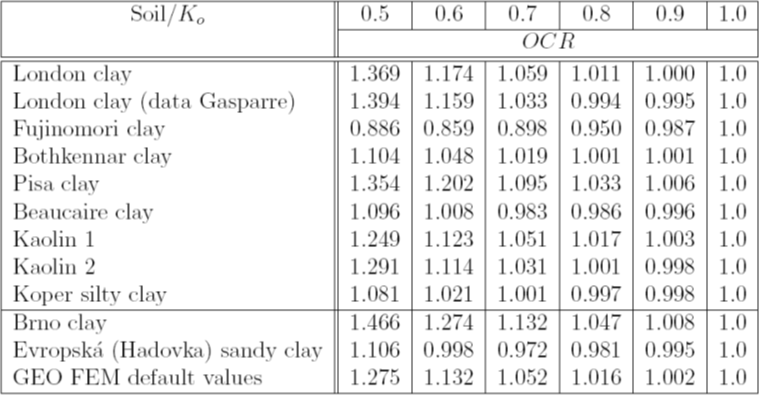表1：不同类型粘土其超固结比OCR大小和Ko值的对应关系

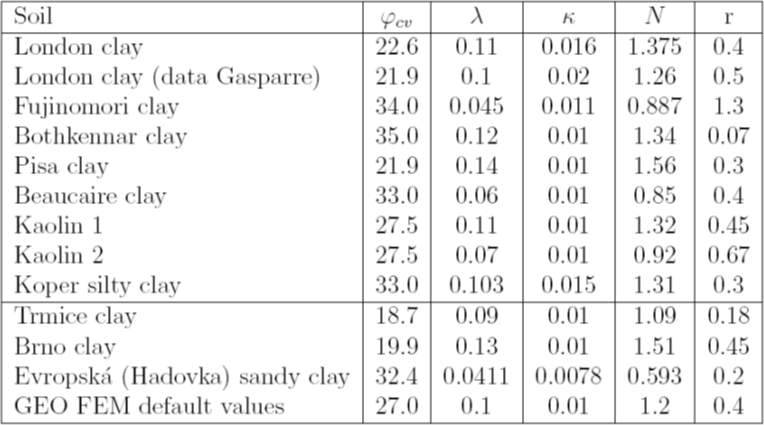表2：各种类型粘土的材料参数

粒间应变

基本亚塑性模型适合于分析应力加载路径沿主方向的情况。当受到循环加载作用时（加载-卸载-再加载），引入粒间变形的概念，并采用了一个更高级的方程。这样就能约束在循环加载时材料塑性（永久）变形的不断增加（棘轮效应）。引入粒间变形后，便可以很好的模拟大刚度的材料，粘土在小应变时刚度往往很大。GEO5有限元分析软件中的其他模型都没有粒间应变的概念。粒间应变的概念认为岩土体的总应变是粒间接触层的微小变形（粒间应变）和土颗粒骨架重新分布的结果。当改变加载路径时，将首先改变粒间应变。当粒间应变达到极限状态后，变形就开始由土颗粒骨架的再分布决定。

采用粒间应变的概念后，将引入另外五个参数：

• 弹性粒间应变的范围R
• 控制小应变刚度的参数m_R和m_T
• 控制剪切应变增加时刚度退化程度的参数β_r和χ

当知道基本亚塑性模型的材料参数后，这些参数需要做一定的调整。

粒间弹性变形的范围R

• 决定了最大粒间应变的范围
• 可以由剪切模量刚度退化曲线得到G = G(ε_s)，如图5
• 也可以将其视为与材料无关的常量R = 10^-4
• 取值范围通常为2_*10^-5 – 1_*10^-4

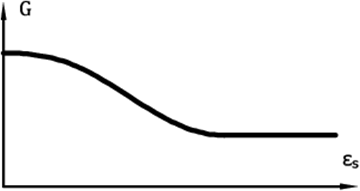图6： 描述剪切模量刚度退化的曲线

参数m_R

• 当改变子午面 (σ_m - J) o 180°上的加载路径时，它决定着剪切模量的大小
• 参数m_R和初始剪切模量G₀的线性关系由下式表示G₀ = p_*(m_r/(r_* λ*)
• 初始剪切模量可以通过剪切波的传播测定[2]
• 取值范围通常为4.0 – 20.0

参数m_T

• 当改变子午面 (σ_m - J) o 90°上的加载路径时，它决定着剪切模量的大小
• 具有如下关系式m_R/m_T = G₀/G₉₀
• 初始的模量比值可以通过大应变时的模量比值估算得到。m_R/m_T的取值范围通常为1.0 – 2.0
• m_T的取值范围通常为2.0 – 20.0

参数β_r和χ

• 决定了剪切应变增加时的刚度退化率
• 可以由刚度退化曲线G = G(ε_s)得到
• β_r的取值范围通常为0.05 – 0.5
• χ的取值范围通常为0.5 – 6

参考文献：

[1] D. Mašín, A hypoplastic constitutive model for clays, International Journal for Numerical and Analytical Methods in Geomechanics., 29:311-336, 2005.