割线模量 Es
割线模量 Es
在各种相关文献中，关于土体模量Es似乎有两种不同的解释。根据Poulos et. Davis (1980) 的说明，Es指土体的弹性模量（杨氏模量），而根据Briaud (2001) 和 Gopal Ranjan (2000) 的说明，Es指土体的割线模量。无论那种说法，模量Es都具有相同的含义。但是，土体往往只在小应变情况下才是完全弹性的，因此，称Es为割线模量更合适一些。
弹性模量E由偏应力-轴应变曲线得到。不排水三轴试验得到的是不排水弹性模量Eu，排水三轴试验得到的是排水弹性模量Ed。
在土体应力-应变曲线的初始阶段，应力应变为线性关系，即土体处于完全弹性变形状态，但是相对于土体的总变形来说，完全弹性变形只是非常小的一部分。针对应力应变曲线，我们可以定义三种不同的模量 - 切线模量、割线模量和初始切线模量。引入这些模量的好处在于可以更方便的利用弹性理论来确定土体的应力应变状态。
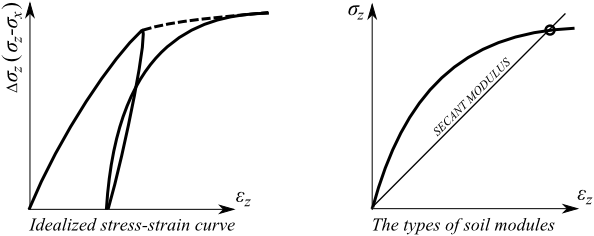理想应力-应变曲线和不同的土体模量
割线模量Es为土体法向偏应力和对应的轴向应变的之比，如下式：
Lambe et. Whitman (1969) 指出土体弹性模量通常为应力应变曲线上零法向偏应力点至二分之一或三分之一最大法向偏应力点的割线模量。
随应变的增大，割线模量Es将减小，因为应力应变曲线是向下弯曲的。可以通过三种方式来获得岩土体的割线模量：
- 室内三轴试验（通过土体的切线模量计算得到）
- 桩基静载试验
- 地区经验公式
除了岩土体本身的变形性质，其割线模量还和其应力历史、含水量、密实度等有关，不同岩土体类型的割线模量Es建议值如下表（Gopal Ranjan et. Rao, 2000）：
岩土体类型 | 土体的稠度或密实度 | Modulus Es [MPa] |
淤泥 | 流塑 | 0,2 – 2 |
黏土 | 流塑 | 2 – 15 |
软塑 | 5 – 25 | |
可塑 | 15 - 50 | |
硬塑 | 50 - 100 | |
坚硬 | 25 - 250 | |
砂土 | 松散 | 7 - 21 |
中密 | 10 – 24 | |
密实 | 48 – 80 | |
砂砾石 | 中密 | 50 – 145 |
密实 | 100 – 190 |
参考文献：
Briaud, J.-L.: Introduction to Soil Moduli. Geotechnical News, June 2001, BiTech Publishers Ltd, Richmond, B.C., Canada.
Gopal Ranjan et. A. S. R. Rao: Basic and Applied Soil Mechanics. New Age International, 2000, chapter 10.11, pp. 328 – 330. ISBN: 8122412238, 9788122412239.
Lambe, T. W. et. Whitman, V. R.: Soil Mechanics. New York: John Wiley and Sons, 1969, 576 p. ISBN: 978-0-471-51192-2.
Poulos, H. G. et. Davis, E. H.: Pile Foundations Analysis and Design. New York: John Wiley and Sons, 1980, chapter 5.5, pp. 101 – 104.
