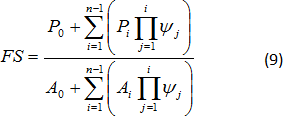不平衡推力法
不平衡推力法
不平衡推力法属于极限平衡法的一种，它只考虑各条块的静力平衡，不考虑其力矩平衡。该方法的基本假设如下图所示。
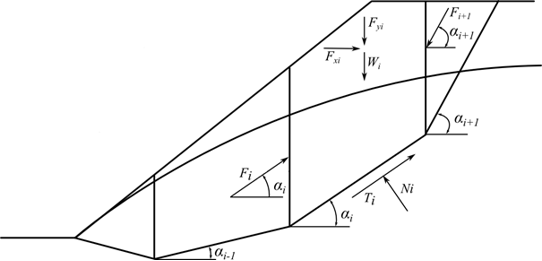图1 作用在某一条块上的力系
基于该方法的基本假设，作用在第i计算条块上的各作用力如下：
其中： | Wi | - | 第i计算条块的重量，条块地下水以下部分采用岩土体的饱和容重γsat |
Fyi | - | 作用在第i计算条块上的竖向外部作用力 | |
Fxi | - | 作用在第i计算条块上的水平外部作用力 | |
Fi, Fi+1 | - | 条块间作用力，其作用方向分别为αi 和αi+1 |
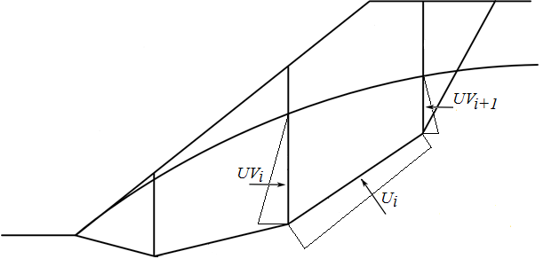图2 作用在某一条块上的水压力
Ui | - | 作用在第i计算条块滑面上的总水压力 | |
UVi,UVi+1 | - | 条块间的总水压力 |
将水压力UVi和UVi+1考虑到水平外部作用力Fxi中，则滑面上的法向作用力为：
滑面上的切向抗滑力为：
其中： | φi | - | 岩土体内摩擦角 |
ci | - | 岩土体粘聚力 | |
li | - | 第i计算条块的滑面长度 |
第i计算条块产生的剩余下滑力Fi（作用方向和该条块滑面方向相同，即αi）为：
将式（1）和（2）代入（3），即可得到剩余下滑力的表达式如下：
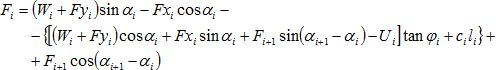
经过一定的形式变换，得到剩余下滑力的另一表达式：
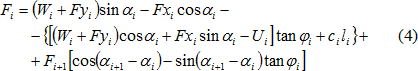
分析中引入安全系数SF对岩土体强度参数c和tanφ进行折减，于是式（4）转换为式（5），如下
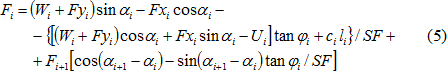
根据式（5），采用迭代法，即可求得安全系数SF。迭代过程中，首先假定SF的初始值，取坡顶第一个条块的条间力Fi+1，即Fn=0 kN，于是由式（5）可以求得第一个条块的条间力Fi，并以此作为第2个条块的Fi+1，依次递推，求出所有的条间力，若坡足条块的Fi≠0 kN，则调整SF的值，反复进行上述计算，直到坡足条块F0=0 kN，此时的SF即为坡体的安全系数。分析时，不考虑滑面上的拉力。如果满足平衡条件时，滑面上的法向力Ni为拉力，即岩土体受拉，那么在下一个迭代步中则取法向力为零，切向力Ti仅由岩土体粘聚力确定。
不平衡推力法对滑面的形状很敏感。当相邻滑面段倾角变化较大时，得到的安全系数通常会比真实的安全系数偏大。相关文献建议相邻滑面段的倾角变化以不超过10˚为宜。分析时，软件会自动检测相邻滑面段的倾角变化，当变化量较大时，软件会弹出警告窗口，提示用户计算结果可能偏危险。对于圆弧滑面，由于滑面平滑，通常不会出现上述问题，但是对于折线滑面，当滑面非常不平滑时，往往会出现上述问题。
不平衡推力法 – 显式解
不平衡推力法显式解采用了另外一种方式来定义安全系数，隐式解中安全系数用于折减抗滑力，而显式解中安全系数用于增大下滑力。调整安全系数为增大下滑力的系数以后，求解安全系数的过程就不再需要迭代，只需一步便能求解出整个坡体的安全系数。显式解所得到的安全系数往往偏大，尤其是当相邻滑面段的倾角变化较大时。
显式解在式（4）的基础上将下滑力乘以安全系数SF，即作用方向沿滑动方向的力，于是得到以下等式：
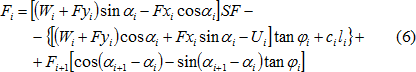
为了更清楚的说明显式解原理，我们定义下滑力如下：
定义抗滑力如下：
传递系数如下：
于是，可以将式（6）简化为以下形式：
下一步，假设坡顶条块Fn=0 kN，于是便可以求出各条块的条间力F：
以此类推
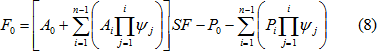
由于坡足条块F0=0 kN，于是得到安全系数SF的表达式如下：
