桩侧摩阻力

桩侧摩阻力通过施加在桩每个分段上的弹簧来模拟。弹簧的刚度由Winkler-Pasternak弹性地基梁模型参数C₁和C₂确定。C₁和C₁由桩周土的变形模量E_def计算得到，并和变形计算深度有关。桩侧弹簧的变形计算深度随桩沉降量的变化而变化。如果桩沉降量为零，变形计算深度为1x桩径；如果桩沉降量恰好为达到桩极限侧摩阻力的沉降量，变形计算深度为kx桩径，其中k为某指定值，这里取2.5。

变形模量是计算C₁和C₂的重要参数。因此，当根据规范中的建议值来选取岩土体变形模量E_def的值时，应当注意建议值是否适用于当前的情况。在某些特殊情况下，例如桩很长时，由于桩埋深很深，桩底岩土体的刚度将远大于规范给出的建议值，尤其是对于粘性土，该特点更加明显。因此，试验数据依然是最可靠的，如果有条件，尽量采用试验数据。

桩侧摩阻力的强度通过相应的弹簧刚度来模拟。弹簧刚度由相应的弹性地基（桩周土）参数计算得到，如下式。不同的桩截面类型，其相应的弹簧刚度计算公式并不相同。对于软件中已经内置的桩截面类型，其对应的弹簧刚度计算公式如下：

圆形截面：

参数α由下式计算得到：

矩形截面：

其中a，b为矩形截面的边长，C₁和C₂为弹性地基参数，k_red为考虑矩形长细比影响的刚度折减系数。

刚度折减系数由下式计算得到：

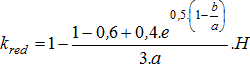
其中a为矩形截面宽度（短边），H为变形计算深度。

十字型截面，I型截面：

这两种截面的弹簧刚度可以由矩形截面的弹簧刚度减去相应四个“挖空”区域的弹簧刚度得到，如下式。

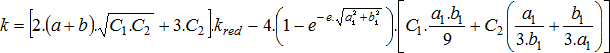
a₁，b₁ - 如下图所示