Shahunyants法
Shahunyants法
Shahunyants法是在极限平衡基础上发展而来的一般条分法。此方法需要作用在每个条块上的力和力矩同时满足平衡条件。通过土条间接触面将滑动面上方的土体划分为若干条块。各条块上的作用力如下图所示：
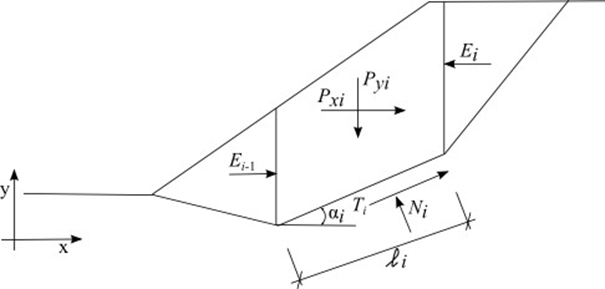静力图 - Shahunyants 法
每个条块假设承受以下作用力：
其中： | Pyi | - | 给定条块上竖向作用力合力（条块重力、表面超载、地震荷载、锚固力等） |
Pxi | - | 给定条块上水平作用力合力（表面超载、地震荷载、锚固力、岩土加固等） | |
Ei+1, Ei | - | 条块之间作用力 | |
Ni | - | 条块底面法向力 | |
Ti | - | 条块底面剪切力 | |
αi | - | 分段滑面的倾角 | |
li | - | 分段滑面的长度 |
Shahunyants 法采用以下假设来计算给定条块的极限状态：
- 条块间的分割面都是竖直的
- 条块之间作用力Ei 的斜率为零，即作用方向是水平的。
求解过程：
首先根据公式 (1) 和 (2)将作用力Pyi 和 Pxi 分解为作用力 Ti 和 Ni 的方向。当 αi 为正角时(如静力图所示)， PNi 的作用方向和 Ni 的作用方向相反， PQi 的作用方向与Ti 的作用方向相反。
(1)
(2)
分段滑面上作用力间的相互关系可以用公式(3)表示：
(3)
其中： | Ui | - | 分段滑面上的孔隙水压力 |
条块上作用力平衡方程：
分段滑面法向平衡条件：
(4)
分段滑面切向平衡条件：
(5)
将公式 (3) 带入公式 (5) 可以得到：
(6)
接着将公式 (4) 带入公式 (6) ：
(7)
通过简化可以得到：
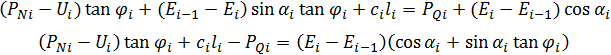(8)
利用下面的数据表达式：
(9)
公式 (8) 可以改写成：
(10)
也可以改写为：
(11)
条块间作用力 Ei 的迭代公式为：
(12)
接着进行安全系数 Ku 分析。安全系数是土体条块上的作用力达到极限平衡状态时的临界值。安全系数是通过增大（乘以安全系数值）不利作用力（滑面以上导致土体滑动的作用力）来得到。公式(12)中不利作用力包含在PQi 项中。此项不仅包含了引起边坡滑动的推力，还包含了阻止边坡滑动的抗力。 推力可以表示为 PQi,sd ，而抗力可以表示为 PQi,ud 。这样公式(12) 就可以变为：
(13)
假设 PQi 值是正的，那么便会促使边坡滑动，因此将会假设为滑动力PQi,sd 。假设 PQi 值是负的，那么便会阻止边坡滑动，因此将会假设为边坡抗力 PQi,ud 。 因此在公式(13)中减去PQi,ud （负值）本质上等于增加了正值， 所以公式 (13) 可以表示为：
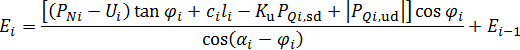(14)
在滑动面起点处 E0 = 0 。 E1 值可以表示为：
(15)
E2 值可以表示为：
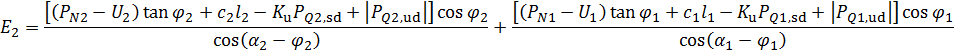(16)
同样，我们确定条块之间所有作用力的大小。最后保证滑动面终点处的 En = 0 。利用先前的表达式可以将此表示为：
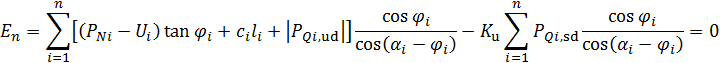(17)
由此方程可以直接得到安全系数 Ku ：
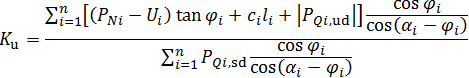(18)
