有限元固结分析原理
有限元固结分析原理
固结
在GEO5岩土工程有限元分析计算软件的标准应力应变分析中,有两种考虑作用在土体上的孔隙水压力的方法。对于不排水条件,假设不排水土体周围的边界条件均为不透水边界,土体的体积恒定,外部荷载完全由超静孔隙水压力承担。引入合适的边界条件,使得超静孔隙水压力逐步消散,则可以过渡到排水条件。对于排水条件,假设土体变形对孔隙水压力没有影响。由不排水条件过渡到排水条件的过程即可以描述为固结。
固结指在外部荷载作用下土体随时间的压缩变形。这是一个很复杂的过程,为了简化问题,这里我们只考虑主固结,即土体孔隙中水分逐渐排出而引起土体压缩的过程。分析时只考虑饱和土,对于非饱和土的固结,软件的当前版本并不予以考虑。控制方程描述了饱和土(![]() ,
, ![]() ) 压缩变形时孔隙水的变化(连续性方程,
) 压缩变形时孔隙水的变化(连续性方程,![]() 表示流量对于时间的导数)。控制方程如下(参考用于描述非稳定流的Richard方程):
表示流量对于时间的导数)。控制方程如下(参考用于描述非稳定流的Richard方程):
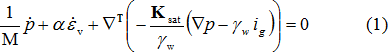
其中: | M | - | Biot模量,假设取值范围为 M = (100-1000)Ksk(Ksk 为土颗粒的体积模量)。通常,M是一个很大的值,从而保证饱和土在固结开始的一小段时间内体积不变。默认设置为 M = 106 kPa. |
α | - | Biot系数,通常取 α = 1 | |
p | - | 孔隙水压力 | |
| - | 孔隙水压力梯度 | |
Ksat | - | 渗透性矩阵,矩阵中为饱和土的渗透系数,各种土体的渗透系数建议值点击这里 | |
ig | - | 水力梯度 |
总应力的变化率由下式得到:
![]()
其中: |
| - | 当前刚度矩阵 |
pex | - | 超静孔隙水压力 | |
| - | 平面应变或轴对称 |
由于总孔隙水压力p为静孔隙水压力pss和超静孔隙水压力pex之和,且:
![]()
因此,连续性方程 (1) 可以进一步由下式表示:

孔压边界取超静孔隙水压力为零作为边界条件:
![]()
水通量密度边界取流量为零(q(t) = 0)作为边界条件:
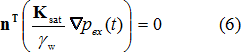
其中: | n | - | 外向单位法向量分量 |
见:设置水力边界条件。
于是,总应力可以由下式表示:
![]()
其中: |
| - | 弹性刚度矩阵 |
ε | - | 总应变向量 | |
εpl | - | 塑性应变向量 |
包含静力平衡方程和连续性方程 (4) 的应力渗流耦合问题可以通过虚位移原理求解,从而得到方程 (7) 中的应变值和超静孔隙水压力值。对于非稳定流分析,采用完全隐式的前向欧拉法对方程 (4) 进行时间离散。详细介绍请见参考文献[1,2,3]。
固结分析
对于非稳定流分析,第一工况阶段用于设置初始条件,即初始地应力和静孔隙水压力的分布。静孔隙水压力同样也等于固结结束时的总孔隙水压力。初始孔隙水压力的分布只能通过输入地下水位来指定。值得注意的是即使地下水位在土体内部,地下水位以上和以下的土体都假设是饱和的。该假设同样适用于后续工况阶段中的填方土体(激活新区域)。挖方(冻结已有区域)在软件的当前版本中是不允许的。固结分析从第二工况阶段开始,需要设置水力边界条件、当前工况阶段的持续时间、时间步数目、荷载加载方式。
设置水力边界条件
软件中允许设置以下两种类型的水力边界条件,参考方程 (5) 和 (6):
- 孔隙水压力为零(p = 0)的边界条件即为透水边界,地下水可以自由流出土体。更确切的说,应当是超静孔隙水压力pex为零,即沿透水边界的总孔隙水压力等于静孔隙水压力pss。透水边界为软件默认渗流边界,即整个模型的所有外边界均为透水边界,如果后续工况阶段有填方,也包括新增区域的边界。
- 水通量密度为零(没有流量,q = 0)的边界条件即为不透水边界。这种边界条件需要用户自行定义。
不同的边界条件设置会影响固结的速率,详细介绍请见参考文献[1]。
设置时间步大小 – 当前工况阶段内期望的时间步数目
不同于非稳定流分析,固结分析中不直接指定初始时间步的大小(解方程 (4) 是采用的时间增量离散值),而是由当前工况阶段的持续时间和时间步数目得到。对于线性固结分析(所有的岩土材料均采用线弹性模型),计算时执行和输入的时间步数目完全相同的时间步数目。对于非线性固结分析,如果当前时间步不收敛,则对当前时间步进行折减,此时,完成当前工况阶段分析所需的时间步数目就会增加。根据工况阶段持续时间长短设置时间步数目时,需要特别注意的是,固结刚开始时,时间步的大小应当较小(尤其是非线性固结分析的加载工况阶段),随着固结的进行,时间步的大小可以增大到几十天。详细介绍请见参考文献[1]。
在分析中加入荷载
对于非稳定流分析,软件提供了以下两种加载方式:
- 当前工况阶段开始时一次性加载。更确切的说,应当是在第一个时间步线性完成加载。如果想要模拟t → 0的情况,则需要设置合适的时间步数目和工况时间,例如时间步数目为1,工况时间为0.01。当时间步很小且为不排水条件(q = 0)时,我们使用一个有限大的剪切模量来模拟土体体积大小不变(K → ∞)的情况。这时,固结分析中t → 0的结果和标准应力应变分析中不排水情况得到的结果将吻合的很好。详细介绍请见参考文献[1]。
- 当前工况阶段内线性加载。荷载增量的大小由当前时间步的大小决定,因此,对于非线性固结分析,需要设置合适大小的的时间步,以防计算结果不收敛。
如果当前工况阶段没有荷载变化,那么上述选项对结算结果没有任何影响。
在固结分析中使用梁单元
梁单元的渗透性由其位置和选择的水力边界条件决定。对于土体内的梁单元,其法向始终为不透水。对于位于模型边界上的梁单元,其法向渗透性由边界的渗透性决定。如果此边界为透水边界(p = 0),那么梁单元法向就透水,如果此边界为不透水边界(q = 0),那么梁单元法向就不透水。
在固结分析中使用接触面单元
分析中使用接触面单元有两层原因。第一,我们希望两种不同的土体之间、土体和岩石之间、或土体与梁单元之间可以有一定的相对位移,例如,分析基坑支护结构和土体之间的相互作用时。第二,模拟沿梁或沿某接触面(更一般的讲,某条线)的渗流情况。因此,固结分析中接触面单元必须实现耦合分析,即应力应变分析和渗流分析同时进行。如果没有指定接触面上的渗透系数,则接触面单元上(法向和切向)的渗流由周围土体的渗透性决定。对于指定到梁单元上的接触面单元,其法向渗透系数kn对计算结果没有影响,因为梁单元的法向渗透性只有不透水(kn = 0)或透水(kn → ∞)两种情况,见“在固结分析中使用梁单元”。
总结
线性固结分析中,各变量,例如沉降、超静孔隙水压力等,将随时间变化,且其变化范围总是以不排水条件(整个分析范围内的所有土体均不排水)下应力应变分析的解和排水条件(标准设置,整个分析范围内的所有土体均排水)下应力应变分析的解为界。后一种情况和超静孔隙水压力完全消散时的情况完全一致,即排水条件下的线性应力应变分析的结果和t → ∞时线性固结分析的结果完全一致。但是,这并不适用于非线性分析,因为非线性分析中叠加原理不再成立。详细介绍请见参考文献[1]。
和渗流分析不同,固结分析中需要使用高阶网格单元,例如6节点三角形单元,或8节点四边形单元。单元的所有节点处均会计算位移(位移场采用二次变化),但是孔隙水压力只在角节点处计算(孔隙水压力采用线性变化)。
不同于“地基固结沉降分析”软件中的一维固结分析,二维固结分析在t → 0时体积应变为零,因此,平均有效应力也为零。位移场的各个分量通常不为零。
参考文献:
[1] M. Šejnoha, T. Janda, H. Pruška, M. Brouček, Metoda konečných prvků v geomechanice: Teoretické základy a inženýrské aplikace, předpokládaný rok vydání (2015)
[2] Z. Bittnar and J. Šejnoha, Numerické Metody Mechaniky II. České vysoké učení technické v Praze, 1992
[3] Z. Bittnar and J. Šejnoha, Numerical methods in structural engineering, ASCE Press, 1996