第二十四章:隧道衬砌有限元分析
本例将演示如何使用有限元方法分析隧道开挖对衬砌的影响。
例题源文件下载地址(v18及以上版本才能打开):http://pan.baidu.com/s/1kVDWjFh
24.1任务
分析在围岩荷载作用下,隧道开挖时其衬砌的变形和受力情况。隧道衬砌的形状如下图所示,其底部深度为 12.0m。衬砌材料为钢筋混凝土,混凝土型号为 C30,厚度为 0.1m。岩土材料参数如下:
- 天然重度: γ = 20.0kN/m3
- 弹性模量:E = 12.0MPa
- 泊松比: υ = 0.4
- 有效内摩擦角: φef = 21.0°
- 有效粘聚力:Cef = 12.0kPa
- 饱和重度:γsat = 22.0kN/m3
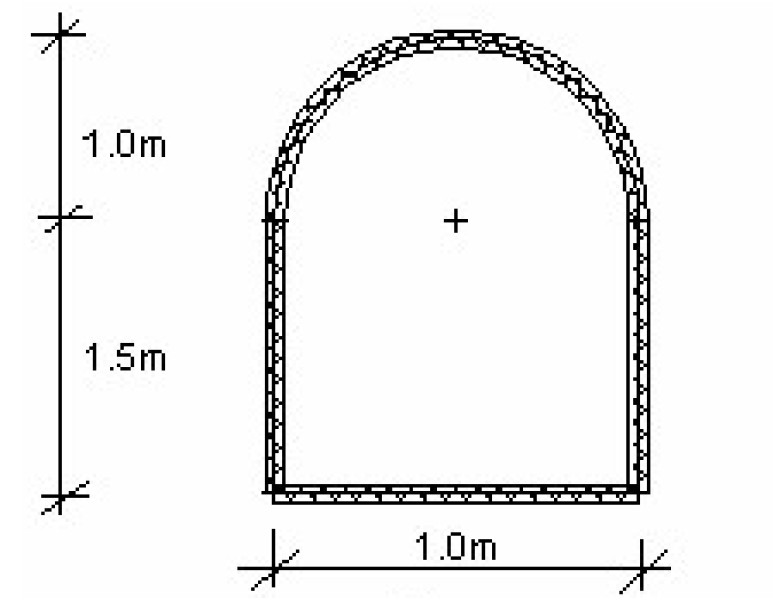
图 24.1 任务描述–隧道衬砌的几何尺寸
对于该算例,我们假设围岩不会发生塑性变形,因此,分析岩土体的应力应变时采用线弹性模型 作为其本构模型。本章的最后,还会采用莫尔-库伦模型来验算岩土体是否屈服。
24.2计算
我们使用“GEO5 岩土工程有限元分析计算模块”(以下简称“有限元模块”)(v18 版)来分析该问题。下面为建模和分析步骤:
- 建模阶段:分析设置和几何建模
- 工况阶段[1]:初始地应力分析
- 工况阶段[2]:添加梁单元,计算位移和内力
- 结论
建模阶段:分析设置和几何建模
在「分析设置」界面中,“初始地应力场的计算方法(第一工况阶段)”选择为“自重应力法”, “项目类型”选择为“平面应变分析”。

图 24.2 「分析设置」界面
设置全局坐标范围和添加地表多段线。设置一个充分大的全局坐标范围尺度,这样才能使得所要分析的区域不受边界条件的影响。对于该算例,设置坐标范围为 <-15m, 15m>,设置模型底边界距离多段线最低点的距离为 20m。
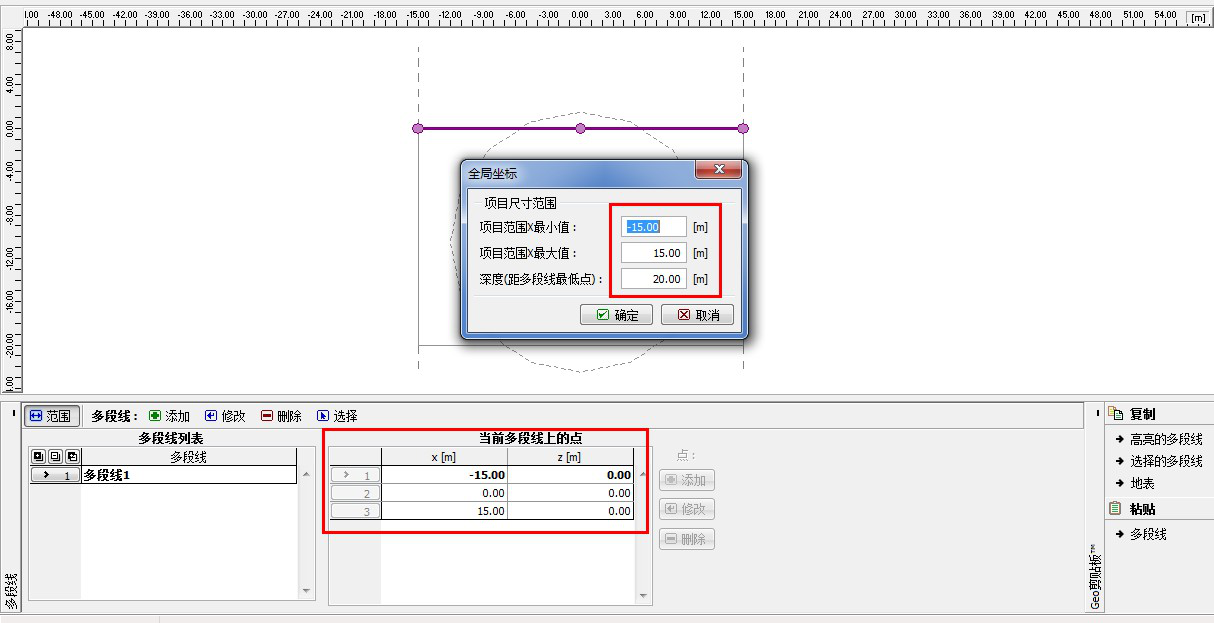
图 24.3 「多段线」界面 +“全局坐标”对话框
进入「岩土材料」界面,在弹出的“添加岩土材料”对话框中选择本构模型,并输入岩土材料的各个参数,然后在「指定材料」界面中将其指定到相应的分区中(详细信息见帮助文档-F1)。
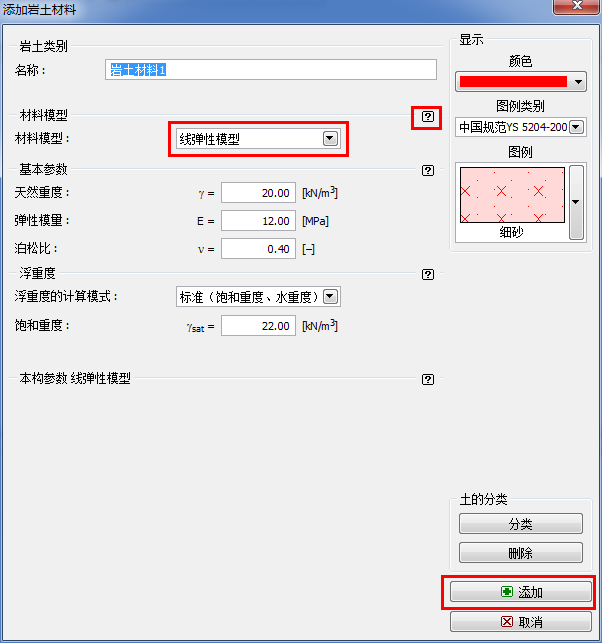
图 24.4 “添加岩土材料”对话框
下一步,创建衬砌结构的几何形状。首先,在「自由点」界面中添加需要的自由点(点击“添加” 按钮),这些自由点即为衬砌的各个角点(详细信息见帮助文档-F1)。
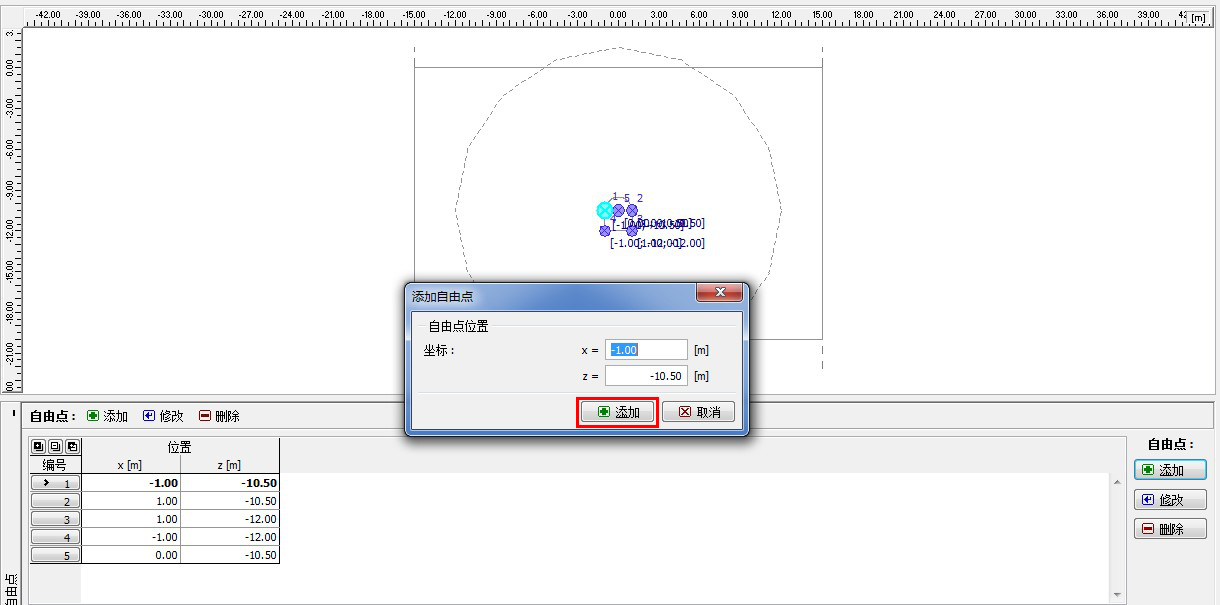
图 24.5 「自由点」界面–“添加自由点”对话框
“自由点”添加完成后,切换到「自由线」界面,点击界面上的“添加”按钮,并使用鼠标将各自由点连接起来(详细信息见帮助文档-F1)。为了将上部直线改为弧线,需要改变线的类型为“弧线”(选择上部直线并点击“编辑”按钮),设置弧形线段的半径为 R=1.0m。
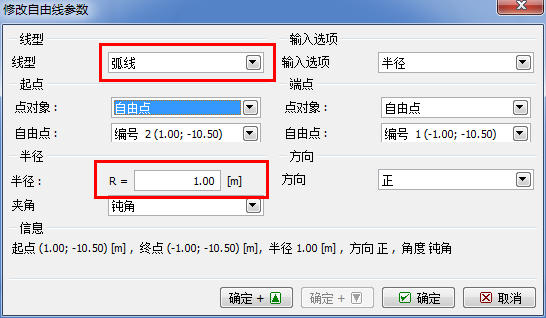
图 24.6 “修改自由线参数”对话框
隧道形状创建完成后,检查是否满足要求。如果没有问题,则切换到「网格生成」界面(详细信 息见帮助文档-F1)。
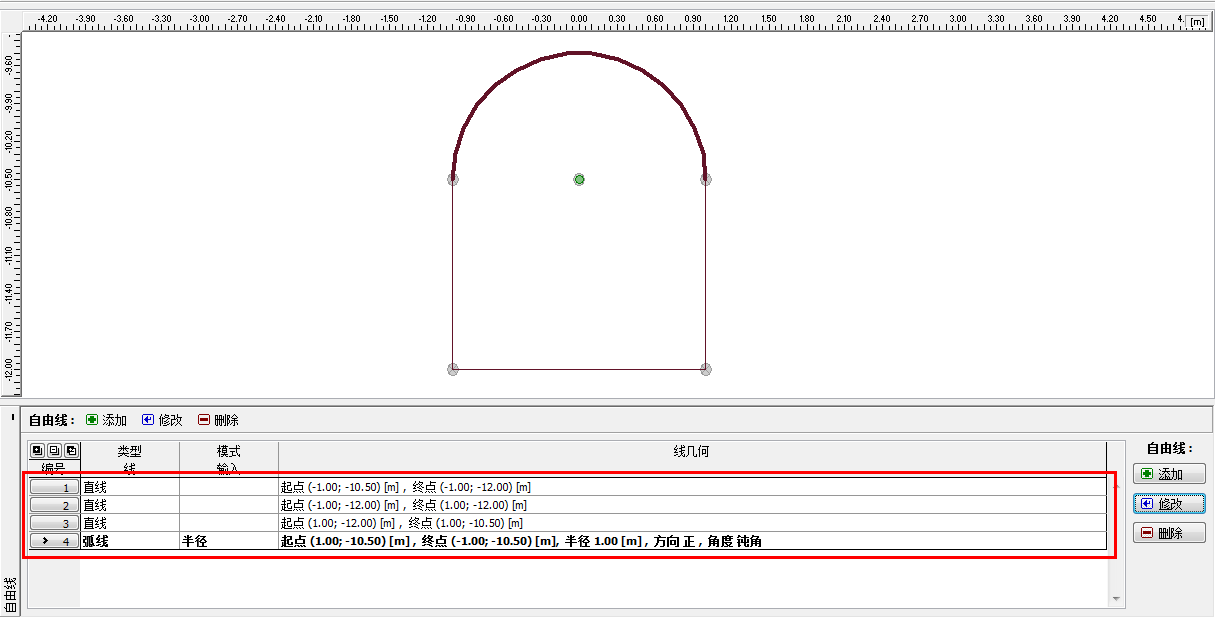
图 24.7 「自由线」界面
生成网格时选择网格边长为 1.0m,点击“启动网格生成”按钮,软件将自动生成平滑的网格。
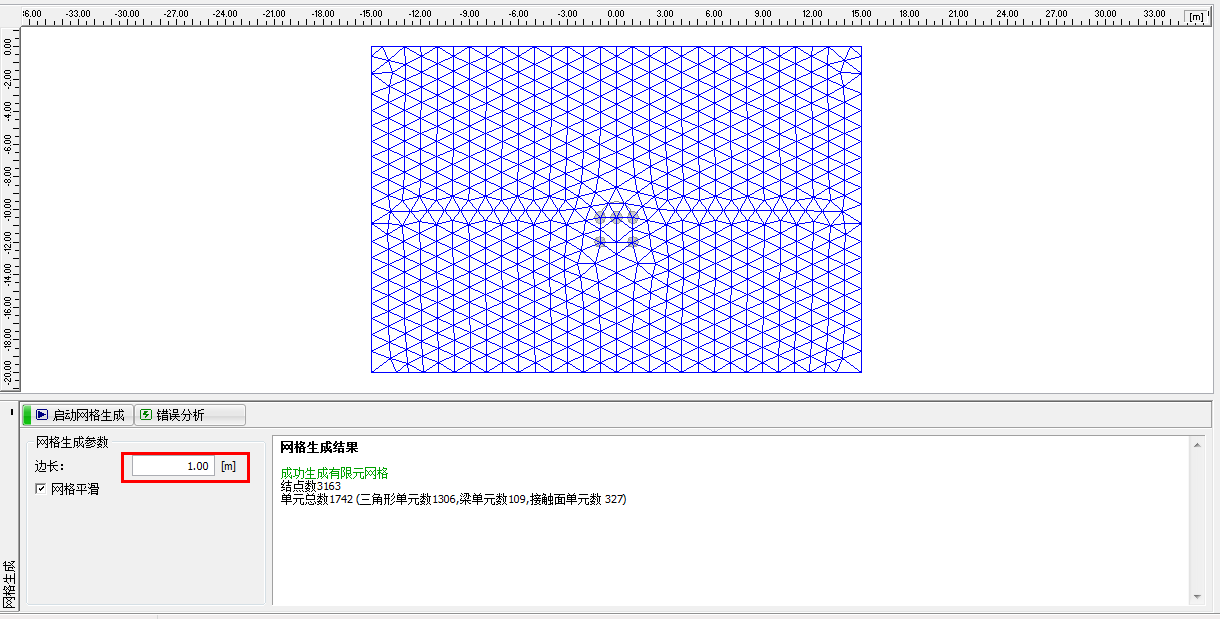
图 24.8 「网格生成」界面–网格边长 1.0m(未局部加密)
很明显,隧道衬砌周围的网格太稀疏,因此,接下来需要对该区域的网格进行加密。加密时,可以围绕某个点进行加密(点加密),也可以选择围绕某条线进行加密(线加密)。对于大部分的隧道开 挖来说,可以采用下面的方法来对隧道周围的网格进行加密:
- 在开挖区域中心附近添加一个自由点
- 以该点为中心进行点加密
图 24.9 “添加自由点”对话框
注:软件计算梁单元在每个网格点处的内力,因此,有必要对梁单元附近的网格进行加密,以保证计算结果的精度(详细信息见帮助文档-F1)。
选择开挖区域中心的自由点为加密中心点,定义加密“影响半径”r=12.0m,“单元边长”l=0.2m。 然后,返回「网格生成」界面,点击“启动网格生成”按钮,勾选“平滑网格”复选框。
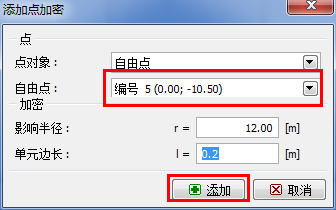
图 24.10 “添加点加密”对话框
注:生成的网格必须达到足够的密度,尤其是可能产生很大应力梯度的区域(例如,支撑点、尖 角区、开挖区等)。进行加密设置时,网格加密影响半径应当至少是要加密区域半径的 3 到5 倍,而 且中心位置的密度还必须和影响半径以外区域的网格密度保持一个合理的比值,这样才能保证网格密 度的平滑过渡(详细信息见帮助文档-F1)。
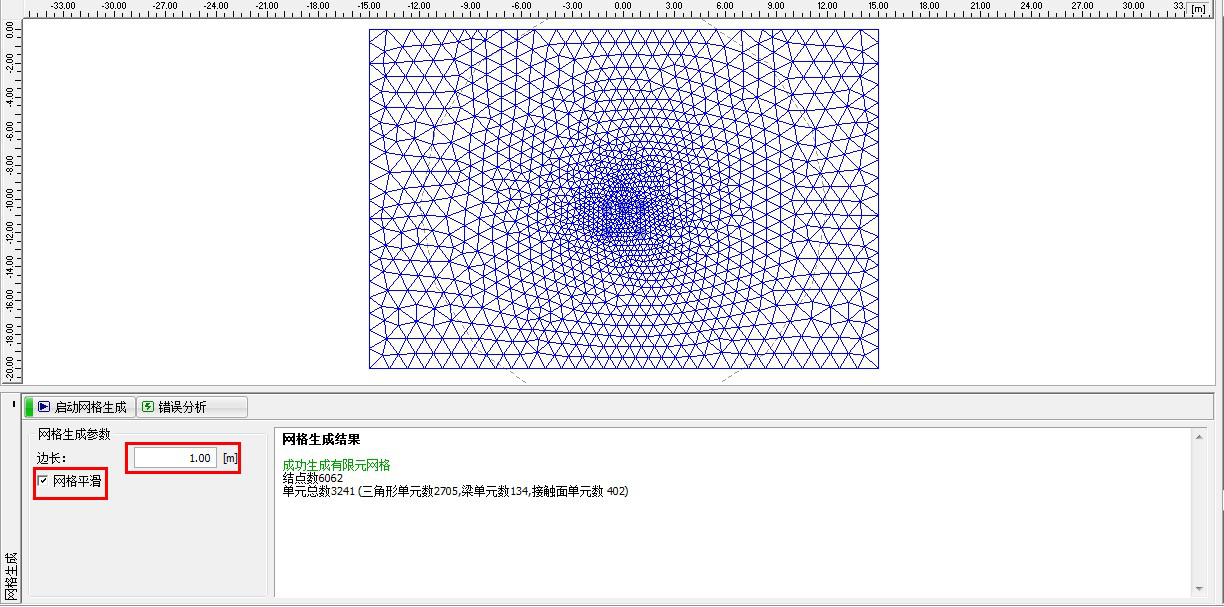
图 24.11 「网格生成」界面–网格边长 1.0m(在隧道中心进行了局部加密)
工况阶段[1]:初始地应力场计算
生成网格之后,隧道区域的网格密度看起来已经足够大,于是进入到工况阶段[1],点击“开始分析”按钮,分析得到初始地应力。分析时的设置选择“标准”,即“默认设置”(详细信息见帮助文 档-F1)。
图 24.12 「分析」界面–工况阶段[1]
工况阶段[2]:添加梁单元
在「激活/冻结分区」界面中,需要模拟隧道中岩土体被挖掉后的状态,于是,设置隧道内部岩土体所在的分区为“冻结”状态(详细信息见帮助文档-F1)。
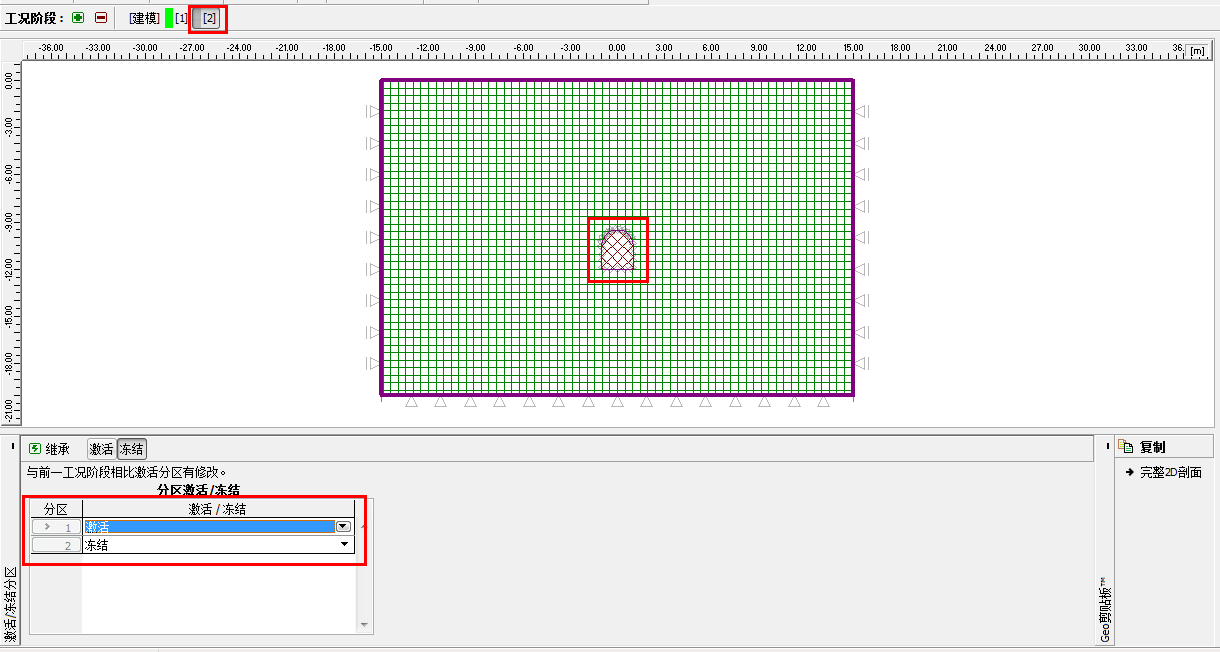
图 24.13 「激活/冻结分区」界面–工况阶段[2]
然后切换到「梁」界面,并输入梁的参数,其中包括梁的位置(自由线)、梁的材料(钢筋混凝土)、混凝土型号(C30)、梁的截面高度(1m)、梁的支座类型(详细信息见帮助文档-F1)。
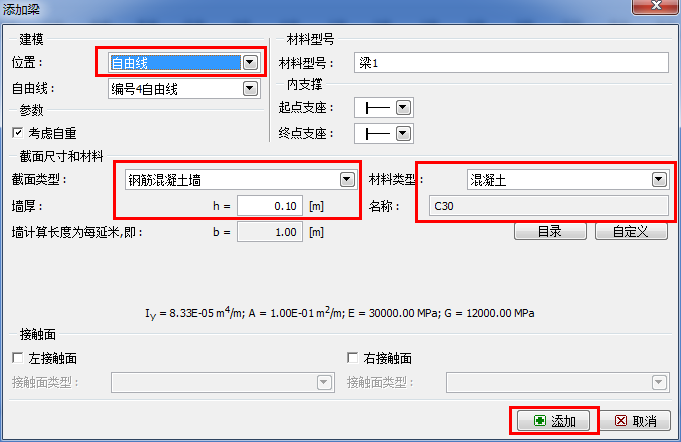
图 24.14 “添加梁”对话框–工况阶段[2]
用于模拟隧道衬砌的所有的梁单元如下图所示。
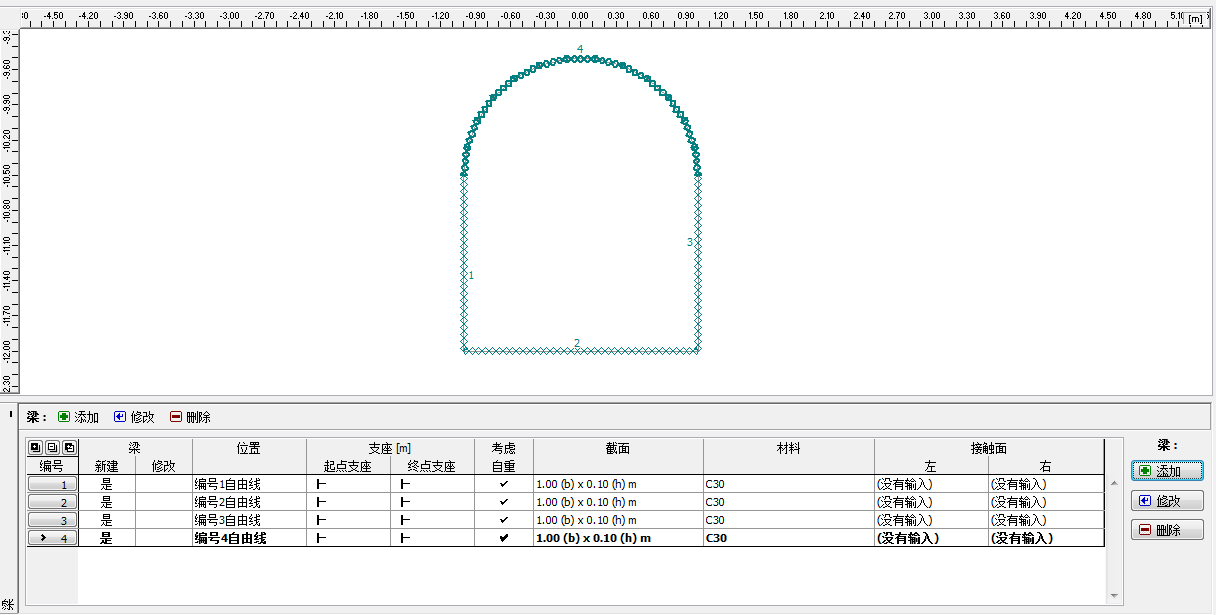
图 24.15 「梁」界面–工况阶段[2]
切换到「分析」界面,点击“开始分析”按钮,并观察分析结果中的 Z 向有效应力 σz,ef[kPa],X向位移 dx[mm]以及隧道衬砌的内力分布。
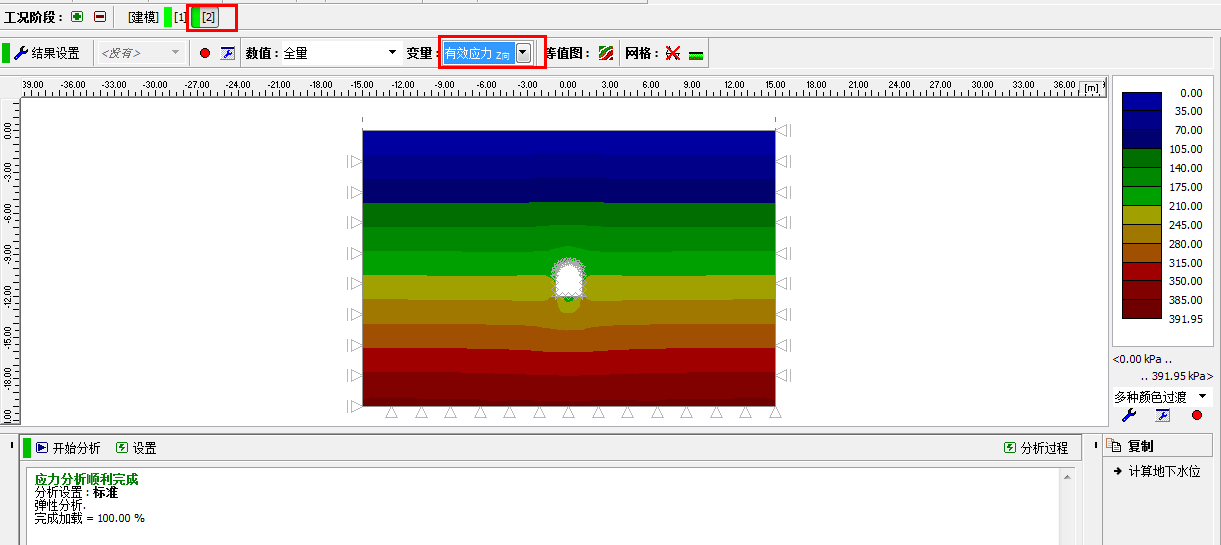
图 24.16 「分析」界面–工况阶段[2](Z 向有效应力 σz,ef)
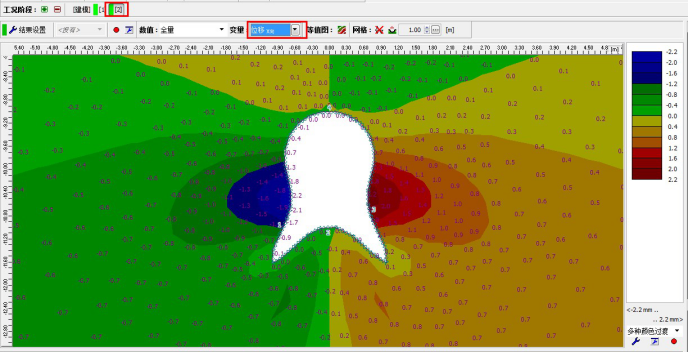
图 24.17 「分析」界面–工况阶段[2](开挖后 X 向位移 dX)
从图中可以看出最大水平位移为 2.2mm(隧道衬砌近似为一个刚性体)。为了更好地了解衬砌的变形情况,选择变形网格图(绘图窗口上方工具栏“网格”标签右侧第二个图标),并且在结果显示 设置中选择显示网格节点上的数值。
注:绘图窗口中显示的各种结果视图可以单独保存下来(通过绘图窗口上方水平工具栏上的红色 按钮实现)。保存之后,还可以通过“结果视图管理器”进行管理,这样就可以快速地在各个不同的 结果视图之间进行切换(详细信息见帮助文档-F1)。
图 24.18 水平工具栏 +“新结果视图”对话框
接下来,查看工况阶段[2]中梁单元(衬砌)的弯矩 M[kNm/m],剪力 Q[kN/m]和轴向压力 N-[kN/m]的分布情况(点击“结果设置”按钮,在“分布力”选项卡中进行设置)。
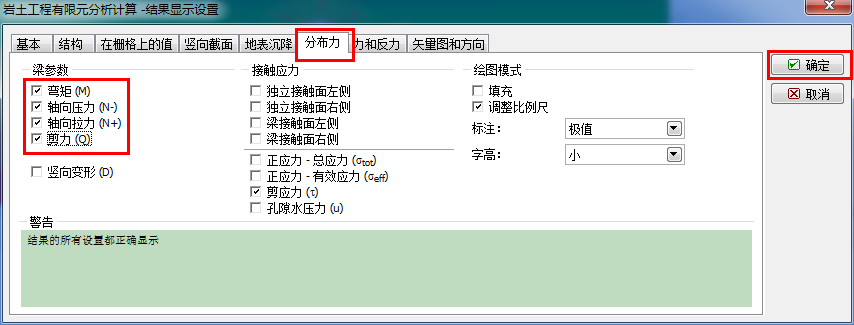
图 24.19 有限元–“结果显示设置”对话框
注:为了使得结果的显示足够清晰,有些计算结果不可以同时显示。例如,不能同时绘制变形网 格和梁单元的内力分布图,一次只能显示其中的一个变量。当设置显示了不可同时显示的变量时,软 件会在结果设置对话框的下方给出一个警告信息(详细信息见帮助文档-F1)。
隧道衬砌的配筋可以通过任意一个静力分析程序来设计和验算(例如,FIN EC-CONCRETE 2D)。 我们将把得到的内力结果记录到一个表格中,以用于配筋设计。
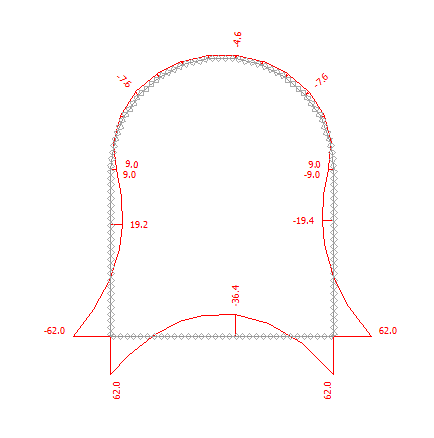
图 24.20 「分析」界面–工况阶段[2](弯矩 M 分布图)
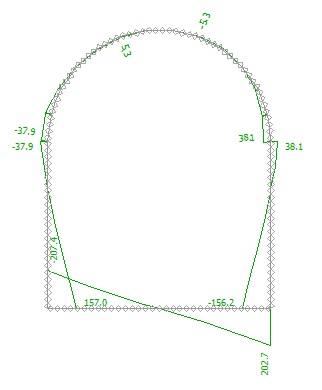
图 24.21 「分析」界面–工况阶段[2](剪力 Q 分布图)
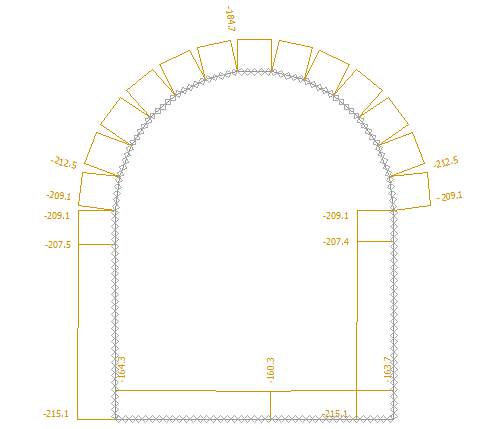
图 24.22 「分析」界面–工况阶段[2](轴向压力 N-分布图)
屈服条件验算:莫尔-库伦模型
现在采用非线性弹塑性模型验算开挖时,岩土体是否产生了塑性变形。返回“建模阶段”,在「岩土材料」界面中把材料模型改为“Mohr-Coulomb 弹塑性模型”。采用相同的方法进行分析,分析完成 后,查看工况阶段[2]中的等效塑性应变。
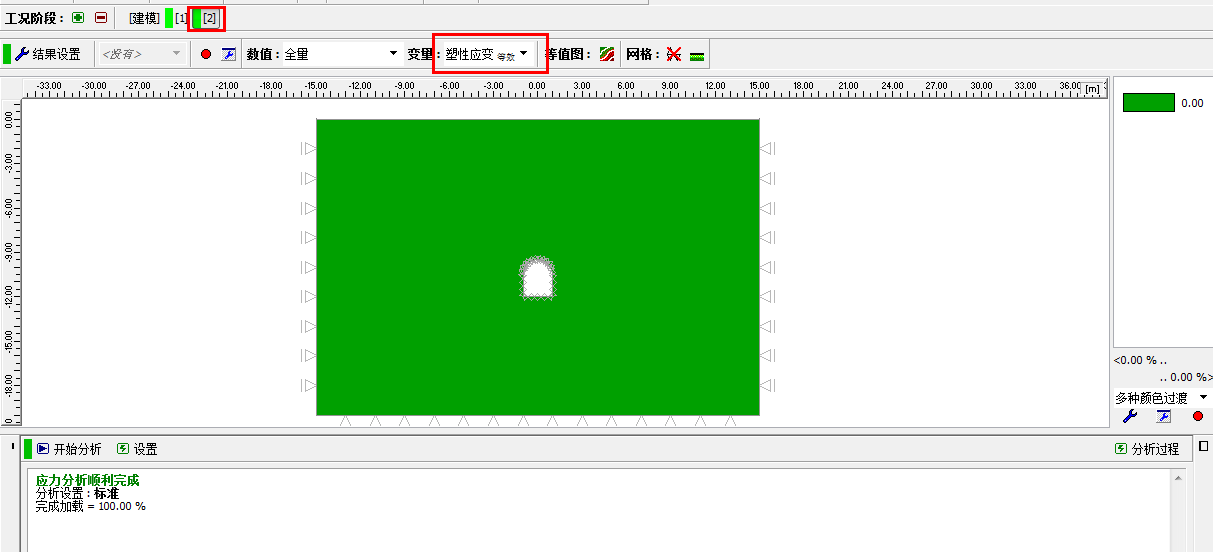
图 24.23 「分析」界面–工况阶段[2](采用莫尔-库伦模型计算得到的等效塑性应变 εeq.,pl)
从上图可以看出,该算例中岩土体的变形尚未达到屈服条件——所有的等效塑性应变 εeq.,pl 都为 0。 这说明采用线弹性本构模型是合理的,因此,前面的分析结果是正确的。进一步的分析可以发现,莫尔-库伦模型计算得到的水平位移、地应力以及梁单元的内力和弹性模型的计算结果是一样的。
结论
下表列出的是工况阶段[2]中梁单元(隧道衬砌)上的内力极值(弯矩、剪力和轴向压力)。分析 时采用线弹性模型,六节点三角形网格,并对隧道区域的网格进行了加密。
表 24.1 梁单元的内力分布(极值)–工况阶段[2]
| 本构模型 | 工况阶段[2] | ||
| N-[kN/m] | M[kNm/m] | Q[kN/m] | |
| 线弹性模型 | -160.1 | +61.9 | +202.6 |
| -215.2 | -61.8 | -206.3 | |
从上面的数值分析可以得出以下结论:
- 在必要的位置加密网格可以得到更为精确的计算结果。
- 如果采用非线性本构模型(例如,莫尔-库伦模型)计算时没有产生等效塑性应变(εeq.,pl=0), 那么材料仅发生弹性变形,此时结构的内力分布、位移和岩土体的应力应变等和采用弹性模 型时的计算结果一致。
注:本算例中的隧道开挖模拟基于这样一个假设,即:岩土体的开挖和衬砌的变形是同时发生的。 如果直接先将支护结构插入到软土中(超前支护),再进行开挖,那么本算例的模拟方法是适用的。 实际情况是,开挖岩土体并进行支护前,岩土体会在无支护的情况下向开挖区域发生一定的变形。第 二六章“新奥法隧道开挖有限元分析”中将通过介绍新奥法隧道开挖的例子进一步说明如何更真实地模拟隧道开挖对围岩和支护结构的影响。
在本算例中,如果开挖之后没有予以支护(不添加梁单元),那么隧道会塌陷掉;如果使用弹性模型计算,会得到非常大的变形量,如果使用非线性模型计算,软件则会提示结果不收敛。
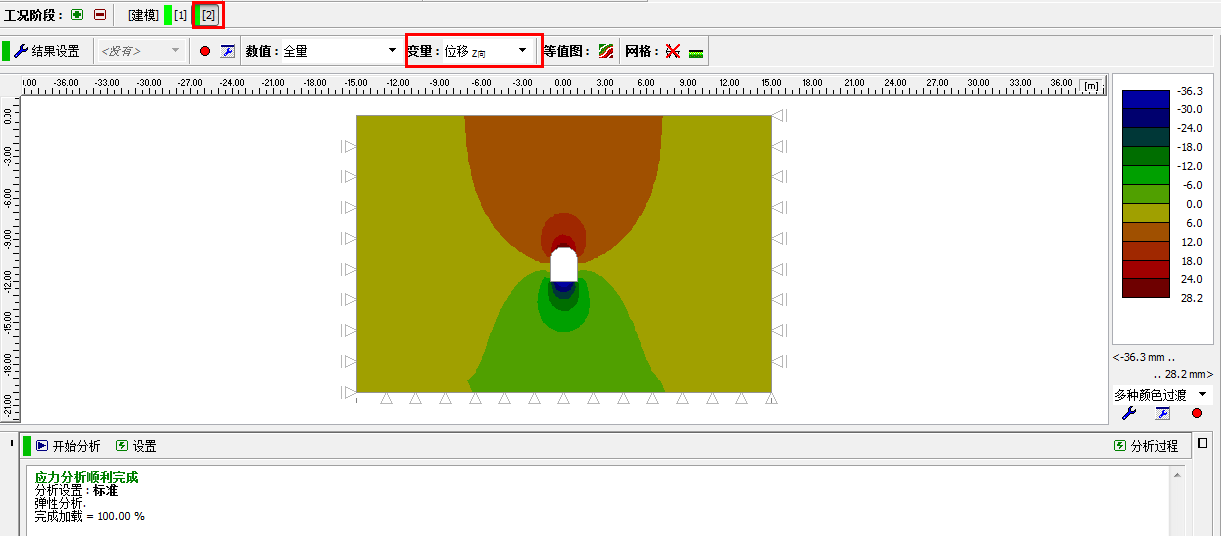
图 23.24 不加入梁单元时的分析结果(使用弹性模型计算得到的 Z 向位移 dz)
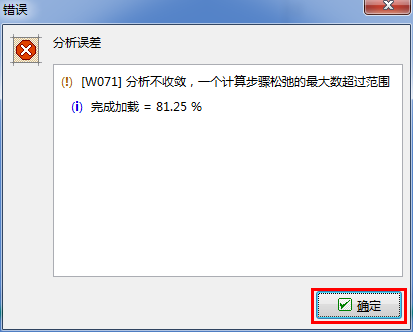
图 23.25 错误提示窗口–不加入梁单元时的分析结果(使用莫尔-库伦模型)