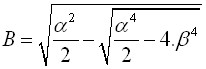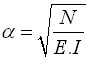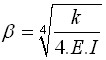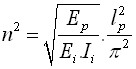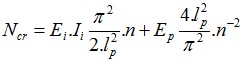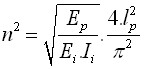Euler几何方法

软件分析中所使用的桩周土特征参数为土的水平反力系数E_p（Winkler常量k），相应的数值由用户在“截面验算”界面中输入。计算结构模型如下图所示：

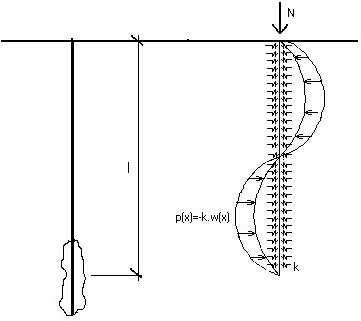结构模型

对于受压微型桩，根据其几何尺寸、结构刚度和桩周土刚度的不同，代表桩身变形的半波数目是变化的。软件的计算结果由完全平直梁的弯曲方程得到：

经过适当的转换后，弯曲方程可以表示成：

积分常数根据假设的桩两端支承方式，由四个边界条件列出的方程组求解得到。

假设两端都为铰接方式连接，可以得到下述方程：

假设为一端铰接，另一端固定的连接方式，可以得到下述方程：

轴向力N_cr由下列方程通过迭代计算得到：