案例66：非饱和土边坡上基础承载力

本案例主要考虑的是土体吸力对边坡上基础长期承载力的影响，如图66.1所示。地下水位的位置意味着从左到右发生渗流，在潜水面之上为非饱和区（潜水面是在分析中由计算来确定的）。土体采用的是默认的硬塑粘土Clay-MC（c ＝10 kPa，φ＝22），采用的水力模型为van Genuchten，参数为 α ＝0.9，n＝1.5。为了检验在计算中土体吸力的影响，将项目下的有效应力设置为太沙基或Bishop，如下图中右下角所示。

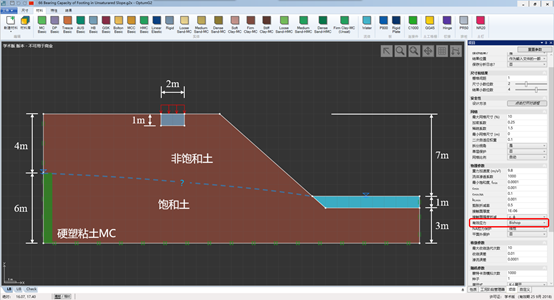
图66.1 非饱和土边坡上基础

根据太沙基理论，有效应力由下式得到：

                                                      σ' = σ - m min(0，p_s)                                                     (66.1)

其中，σ 为总应力，m = (1,1,1,0,0,0)^T ，也就是说，不考虑土体吸力( p_s > 0)。

根据Bishop理论，有效应力由下式得到：

                                                          σ' = σ - Se m p_s                                                          (66.2)

其中S_e是在Van Genuchten模型中定义的有效饱和度（参见材料手册）。在本案例中，当剩余饱和度为0并且最大饱和度为1时，有效饱和度等于通常的饱和度。

现在考虑摩尔-库仑破坏模型：

                                         F = | σ₁ - σ₃ | + ( σ₁' + σ₃' ) sinφ - 2c cosφ                                   (66.3)

这里有：

                                        F = | σ₁ - σ₃ | + ( σ₁ + σ₃ ) sinφ - 2c_eff cosφ                                  (66.4)

其中：

                                                         c_eff = c + Se p_s tanφ                                                     (66.5)

也就是说，对于p_s > 0，吸力的作用可以认为是土体粘聚力增加了 Se p_s tanφ 。在OptumG2中，对于p_s > 0，Se p_s 用吸力 σ_s 表示，可在结果菜单下查看。

进行上下限分析时，采用的单元数量为10000，自适应网格迭代次数为3次，两种情况下的承载力为：

                                             太沙基：q_u = 48.1 kN/m² ± 6.1%                                                               

                                             Bishop：q_u = 87.9 kN/m² ± 3.5%                                            (66.6)

也就是说，由于吸力的作用，使得承载力增加了大约80%。

Bishop情况下的饱和度和吸力分布如下图所示：

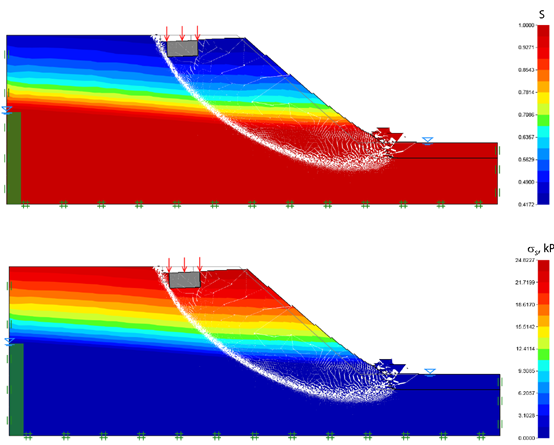
图66.2 破坏时饱和度（上）和吸力（下）随位移的变化情况