案例23：MC砂土上的条形基础

本案例主要介绍的是一个关于深砂层上条形基础承载力的经典问题，如图23.1所示。尽管这个问题看起来很简单，但这个问题，也被称为N_γ问题，被广泛认为是很难得到处理解决的问题。首先，自由曲面和纯摩擦材料的结合使得传统的牛顿-拉夫逊有限单元出现问题，因此，常常需要引入一些不重要的内聚力。其次，基础边缘的点是一个奇点，如果不解决这个问题，可能会导致得到错误的结果。第三，这个问题对摩擦角非常敏感，例如，摩擦角ϕ = 30°和ϕ = 35°，承载力为两倍多；摩擦角ϕ = 35°和ϕ = 41°，承载力为三倍多。最后，应当指出的是，这个问题没有固定形式的解决方案，而且文献中引用的一些公式也存在一些错误。在下面，我们将使用马丁（2005）提供的解决方案，由冯卡门（1926）导出的ODE直接积分来得到结果，这些解决方案对于所有实际用途都是精确的。

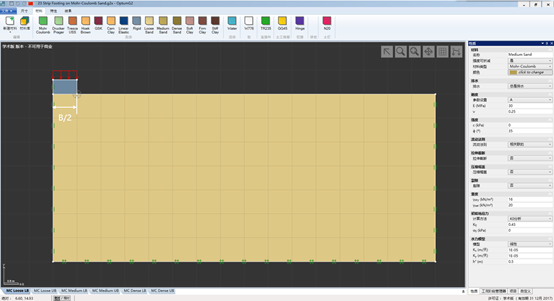
图23.1 MC砂土上的条形基础（采用对称性模拟问题的一半即可）

OptumG2中采用的流程和其他有限元软件在根本上是完全不同的，对于本案例中的问题，这意味着：

• 将内聚力设置为恒等于零。请注意，查看结果中关心的是剪切耗散，而不是总耗散，无论是网格自适应性，还是对结果的可视化。

• 对于所有其他问题，也可以计算上下限解，这直接给出了数值解中的误差。此外，可以发现，上限解和下限解之间的平均值对精确解提供了一个很好的估计——即使边界之间的间隙是显著的。

• 基础边缘的奇异性可以采用特性栏下可用的扇形网格工具来处理。这个特性在奇点的周围添加扇形的网格，这常常可以改进解决方案，特别是对于下限解，如图23.2中给出了一个例子。

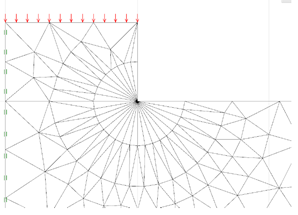
图23.2 基础边缘的扇形网格（10°）

如图23.1所示，砂土上集中荷载条形基础的承载力可以表示为：

                                                            q_u = 1/2 B_γN_γ                                                              (23.1)

其中，N_γ 为何摩擦角相关的承载力系数。对于默认的Mohr-Coulomb松砂、中砂和密砂土料，N_γ为：

                                           松砂  （φ = 30°）：N_γ = 14.7543                                                                 

                                           中砂  （φ = 30°）：N_γ = 34.4761                                                (23.2)

                                           密砂  （φ = 30°）：N_γ = 85.5656                                                                 

为了研究网格自适应和扇形网格在奇点处的相对影响，考虑了四种不同的场景：

a）  没有自适应网格，没有扇形网格

b）  没有自适应网格，有扇形网格

c）  有自适应网格，没有扇形网格

d）  有自适应网格，有扇形网格

网格自适应计算时，自适应迭代次数为4，网格单元数量从1000个单元开始（见第23.1章节）。在所有情况下，扇形网格的角度为10°。

结果如表23.1-4所示，可以发现，虽然加入扇形网格可以明显改善网格加密效果，但它主要是对粗网格的效果相对更好。另一方面，不管有没有扇形网格，网格自适应的效果是非常明显的（也更耗时）。此外，上下限解的平均值为精确解提供了很好的估计。事实上，误差很少大于5%，即使各自的边界相当差。此外，它们通常是安全的，这表明下限解通常比上限解稍差一些。按照c）情况，对于密砂最好的网格和破坏模式如图23.3所示，奇点处的集中变形相当明显。

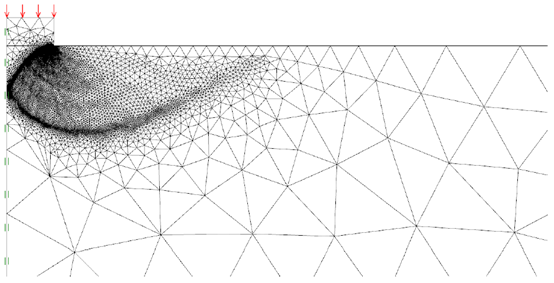
图23.3 中砂抗剪强度的网格划分和破坏模式（下限解）

表23.1 MC砂土上的基础极限荷载，q_u/q_exact，a）无网格自适应，无扇形网格

表23.2 MC砂土上的基础极限荷载，q_u/q_exact，b）无网格自适应，有扇形网格

表23.3 MC砂土上的基础极限荷载，q_u/q_exact，c）有网格自适应，无扇形网格

表23.4 MC砂土上的基础极限荷载，q_u/q_exact，d）有网格自适应，有扇形网格

23.1 网格自适应

在本案例中，我们进行自适应网格设置时，采用4个自适应网格步来取代默认的3步，这些和网格自适应相关的设置，可以通过工况管理器和项目栏的网格类别进行修改（如图23.4所示）。

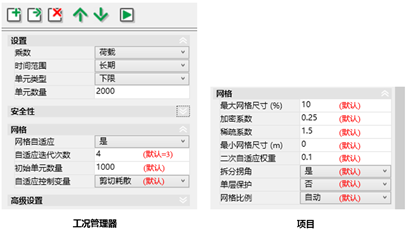
图23.4 网格自适应设置：工况管理器（左）里的设置针对于特定工况，项目（右）里的设置应用于所有工况

使用网格自适应性，其目的是在给定的自适应迭代次数（上述情况下为4次）中，从初始网格数（在上述情况下为1000）一直增加到最终的网格单元数（在上述情况下为8000）。这是在两次迭代过程中，最大单元大小不能超过给定系数的限制下完成的，类似地，最小单元大小受到不能小于预定系数的限制。这两个系数分别被称为稀疏系数和加密稀疏，它们的默认值分别为1.5和0.25。一般来说，这些设置以及其他默认设置，会得到合理的网格划分，得到的上限解和下限解之间的差距是合适的。然而，在某些情况下，则需要更谨慎的策略。因此，限制迭代之间的单元大小的增加/减少通常会得到更可靠的结果，当然，以牺牲更多的自适应迭代次数为代价来达到最终的网格数量。相反，比默认的稀疏和加密系数所代表的更积极的策略也可能是成功的（例如降低加密系数至0.1）。最后，从较少的单元开始（由初始单元数量给出）可能导致一个相当差的建模效果，在此基础上很难划分更好的网格。总之，如果默认设置不能生成所需精度的网格单元数量= 10000或以上的网格，则按优先级顺序更改的设置是：

1、  增加自适应迭代次数（标准值=4）；

2、  增加初始网格数量（标准值=2000）；

3、  减小加密系数（标准值=0.15）；

4、  增大稀疏稀疏（标准值=2.0）。

最后，当Mohr Coulomb、Drucker Prager、Tresca模型中拉伸截止值k_t = 0时，总耗散往往比默认的剪切耗散更适用于自适应控制，尤其是使用下限单元的时候。