案例55：粘土中螺旋锚杆的抗拔能力分析
本案例对粘土中的螺旋锚杆进行抗拔分析，如图55.1所示。锚杆采用如图中所示的轴对称的板单元来模拟，锚固体的嵌入深度为H，板单元之间的间距为S，所有锚板单元的直径为D。板单元与土体之间的接触面假定为“平滑”，但能够维持张力，这通过将界面折减系数设置为零来实现（如下图所示）。更多详细的界面条件的讨论参考案例27。
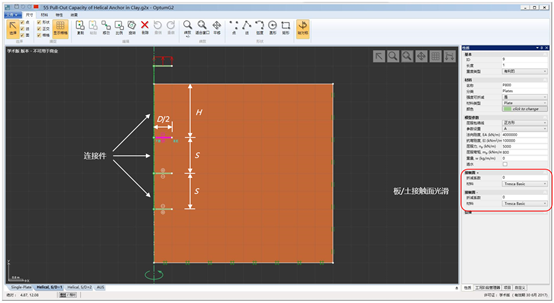
图55.1 螺旋锚杆
土体为Tresca模型，具有恒定的剪切强度Su。假设土体和锚杆都处于失重状态，抗拔能力可以表示为：
(55.1)
其中，Q是总拉拔力，Nc是抗拔系数，本案例会讲到Nc如何确定。
55.1 单板锚杆
首先考虑嵌入在距离地面距离为H的单板锚杆，Nc随着深度的增加而增加，直到破坏模式不再与深度的增加有关。此时，对于所有更大的嵌入深度，Nc由下式来表示（Martin和Randolph，2001）：
Nc = 3 + 3π ≌ 12.42 (55.2)
抗拔系数Nc随着标准化深度H/D的变化曲线如图55.2所示，这些结果基于极限分析的上限分析和下限分析得到的，网格数量为10,000个，迭代次数为3。可以看出，H/D值达到一个足够大的值之后，Nc结果与Martin和Randolph（2001）的结果非常一致。
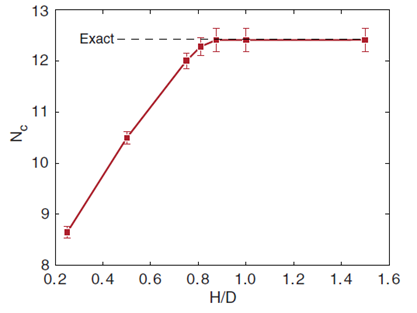
图55.2 抗拔系数随深度的变化曲线（上限解和下限解的平均值）
从全局到局部破坏机理的变化过程如下图55.3所示。
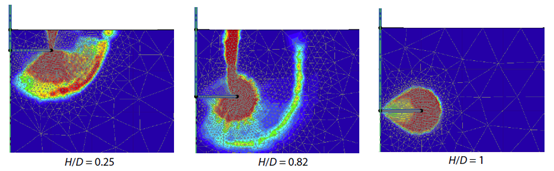
图55.3 从全局（浅）到局部（深）破坏机理的变化过程
55.2 多板锚杆
接下来，考虑三板锚杆的情况，如图55.1所示。从定性角度来看，埋深深度的影响和单板锚杆保持一致：对于埋深较小时，破坏机理是全局型的，可达到地表；对于足够大的埋置深度，破坏机理是局部型的，相应的抗拔系数Nc为一固定值。
此外，板间距对浅层和深层的状态都会产生影响。S/D值足够小时，板之间会存在显著的相互作用；而对于S/D值较大时，板基本上是独立的。当S/D值达到某一较大值时，抗拔系数Nc为一固定值，对此Merifield（2010）提出了表达式55.3：
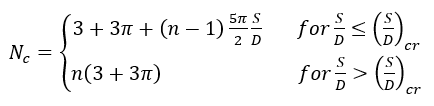(55.3)
其中，n是锚板的数量（在本案例中n＝3），间距比S/D的临界值表示范围之间的切换，锚杆作为一种有效的单板锚杆，锚板则是对应与n个单板锚杆独立作用。临界间距比由下式55.4表示：
(55.4)
图55.4呈现的是两个间距比分别为S/D = 1和S/D = 2的螺旋锚的抗拔能力。当H/D值较大时，Merifield对于Nc的表达式与计算结果吻合良好。
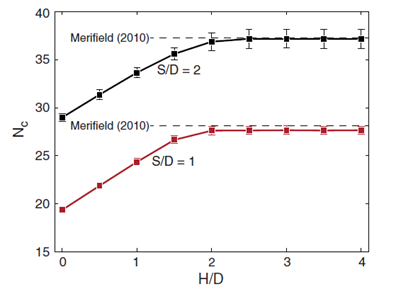
图55.4 螺旋锚杆的抗拔能力
H/D = 4时的失效机理如图55.5所示，对于S/D＝1时（低于临界比值），锚杆表现为一个有效的单板锚杆；当S/D＝2时（超过临界比值），意味着三个锚板作为三个单板锚杆来起作用，在这种情况下，抗拔能力是单板锚杆的三倍。
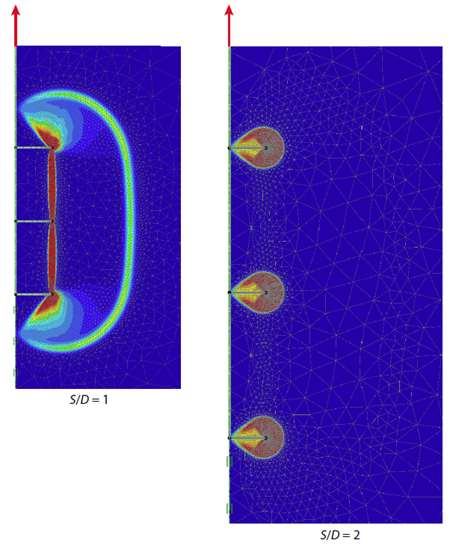
图55.5 S/D=1和S/D=2时螺旋锚杆的深度破坏机理
55.3 AUS分析
在本案例中，锚板假定是光滑的，即在板和土之间不存在剪切作用，但是正常应力，包括拉应力，仍然存在，这意味着板顶部的土体将处于压缩状态，而底部的土体将处于拉伸状态（如图55.6所示）。这也就是说，在压缩和拉伸不排水抗剪强度之间的任何差异都可能对抗拔能力产生相对显著的影响。正如材料手册中所讨论到的，两种抗剪强度之间的差异是准则而不是例外，因此研究这种影响对锚杆整体抗拔能力的影响是非常有必要的。
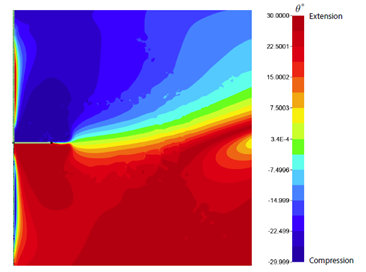
图55.6 锚板附近的洛德角θ的变化（单板锚杆），θ= -30°对应于压缩，θ= +30°对应于延伸
相关分析可采用AUS模型来进行，输入的参数为压缩和拉伸不排水剪切强度（也可以直接选择剪切强度）。在随后的模型中，各向同性用来分析对应于深度破坏的H/D值的单板锚杆，本模型分别通过压缩强度和拉伸强度来运行，即suc和sue。抗拔系数Nc和suc/sue的关系如图55.7所示，可以看出，在suc/sue=0.5和suc/sue=1之间，随着抗拔系数Nc的增长（约50%），suc/sue比率具有显著的影响。
图55.7 抗拔系数Nc（对应于深度破坏）随着不排水抗剪强度率suc/sue的变化曲线
同时可以看出，suc/sue对应的结果略低于Martin和Randolph（2001）的结果。这是由于非结合性的影响：当suc/sue=1时，AUS破坏面对Tresca表面进行折减，流动法则符合von Mises模型。因此，抗拔系数Nc略有下降，从约12.4（破坏面和流动法则采用Tresca模型）降到约12（破坏面和流动法则采用AUS模型）。
