案例13：悬臂式挡墙的稳定性

本案例看似并不复杂，可以采用上一章中类似的方法进行模拟。挡墙形式为悬臂式，如图13.1所示。土体采用软件默认材料「中密砂土-MC」模拟（无黏性Mohr-Coulomb材料，摩擦角为 35°，重度为16 kN/m³），挡墙采用刚性材料模拟，重度为 20 kN/m³。

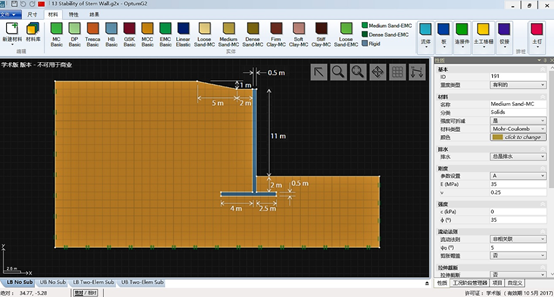
图13.1 悬臂式挡墙

和上一章中的案例一样，采用「强度折减」分析得到基于强度折减的安全系数FSs。我们采用不同的网格单元数量且不进行网格自适应，得到安全系数的上限解和下限解。

表13.1 细分和不细分悬臂式挡墙时的强度折减系数

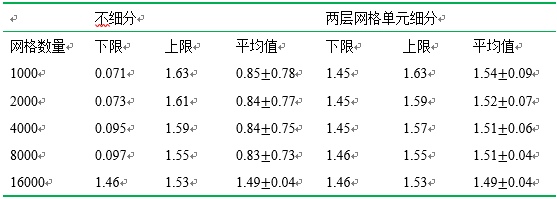
从表13.1左侧的结果中可以看出上限解和下限解之差非常大，直到网格单元数量达到16000时，两者之差才突然大幅减小到可以接受的程度。更准确的说，除表中最大数量的网格外，其余情况中下限解的质量都非常差，且均意味着结构非常不稳定。另外一方面，上限解则相对更合理和稳定。

仔细查看不同网格数量下的网格划分情况，可以发现 1000到 8000网格数量下沿挡墙宽度方向只有一层网格。当网格数量达到 16000时，挡墙的大部分区域都有两层网格。如果没有对刚性区域进行合适的处理，该区域将对下限解产生非常不利的影响，这点已经被大量学者证明。事实上，由于下限解要求应力场要满足平衡方程的强形式，所以整个模型的所有区域 – 无论是刚性区域还是变形区域 – 都必须要有足够的网格划分以保证求解得到的应力分布能达到合理的精确度。另一方面，上限解只需要满足外部功率和内部功率的平衡，而刚性区域没有内力做功，所以上限解对刚性区域的网格划分要求不高，上述计算结果已经证明了这一点。

在本案例中，通常情况下提高下限解精度的方法就是用更多的网格单元来对墙体进行离散。在OptumG2中，只需要用一条线把挡墙进行划分即可以很容易的实现，如图13.2所示。这条划分线保证了沿墙宽方向至少有两层网格，从表13.1中可以看出，采用两层网格划分挡墙后的计算结果精度大大提高了。从计算结果中也可以注意到，不对挡墙进行人工划分时，即使采用网格自适应，得到的下限解也很不理想，因为网格自适应的计算建立在一个较为合理的初始解基础上。

除了人工划分挡墙，也可以使用「特性」界面中的「网格大小」工具来指定划分挡墙的最大网格大小。最大网格大小一般设置为墙宽的1/3到1/2。对于本案例，最大网格大小设置为 0.25 m（墙宽的一半）即可以保证沿墙宽方向为两层网格划分（如图13.2所示），从而满足计算精度要求。

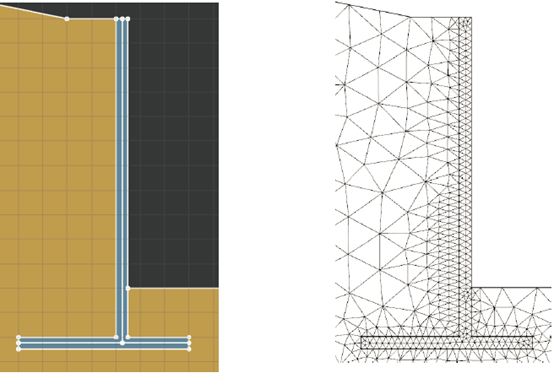
图13.2 人工划分挡墙（左）和指定墙体最大网格为 0.25 m的网格划分结果（右）