案例29：荷载-位移分析—入门案例

本案例介绍了乘数弹塑性分析类型的荷载-位移分析。这种类型分析是基于OptumG2特有的一个算法，它是在Sloan等（2000）之前使用传统算法结果的基础上得到验证的。验证示例如图29.1所示，考虑两种情况：关联流动(φ= 30°)和非关联流动，且剪胀角ψ减小到20°。在这两种情况下，采用Mohr-Coulomb土体模型，c = 1 kPa，E = 1.04 MPa，v = 0.3，土体和基础都是失重的。

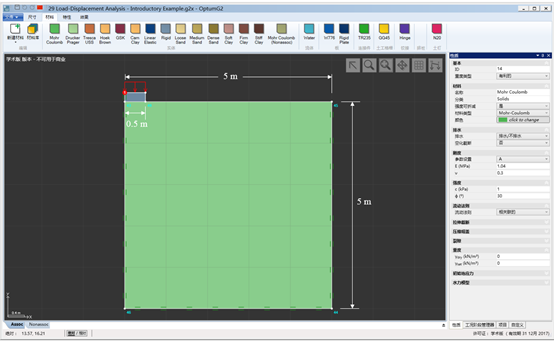
图29.1 施加于失重的Mohr-Coulomb地基上条形基础的分布荷载

29.1 乘数弹塑性分析设置

乘数弹塑性分析需要定义一个或多个乘数载荷（集中荷载、分布荷载或体荷载），乘数载荷的大小将逐渐增加直到达到承载力临界值，或者通过适当的设置，直到达到预定的荷载或位移为止，相关设置可在工况管理器的高级设置下进行。另一方面，固定荷载则在整个分析中保持为指定的固定值。

荷载步是通过工况管理器设置里面的三个参数来控制，分别是：N_E、N_P和β。典型的荷载-位移曲线如图29.2所示，可以发现曲线最初近似于线弹性，然后逐渐变得越来越趋于塑性。N_E和N_P指定了这两个区域的大致步数，参数β用来步与步之间的荷载步的自动调整。对于β= 1，步长（工作时测量）不会变化，而更高的β值则意味着一个更积极的策略，随着步长的增加，部分曲线几乎没有变化。对于大多数问题，默认参数，N_E = 10，N_P = 10和β= 5，是一个很好的起点，增加荷载步的数量（即增加NE和NP）通常不会导致太大的改进。

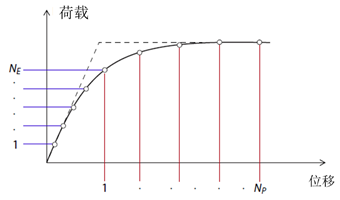
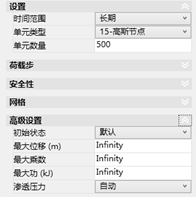
图29.2 典型荷载-位移曲线（左）和设置区域（工况管理器）

初始应力可以在一个单独的工况阶段计算，然后通过“从”工况将其与乘数弹塑性工况联系起来。或者，如果没有指定“从”工况，高级设置下的初始状态选项提供了很多计算初始应力的选项。三种选项分别是：

1、默认。通过初始应力分析可以自动计算初始应力（见第I、II），所有乘数负载在这个阶段都被忽略。

2、自动。此设置与初始不稳定的问题有关，除非乘荷载载不同于零。在弹塑性计算的基础上，计算了达到稳定状态的应力场和最小荷载乘数。

3、人工。此设置和自动相当，除了初始荷载乘数由用户来指定。

如果指定了“从”工况，初始应力仅仅是来自“从”工况的最终应力。

在下面，没有指定“从”工况，使用的是默认选项。

29.2 数据记录

在加载过程中通常会记录各种数据，例如在某些点上的位移。在OptumG2中，如果在某一点定义记录该点位移、应力和其他各种量的结果点，荷载乘数会自动记录下来，之后可以使用结果栏中的XY绘图工具绘制这些结果。

29.3 结果

使用15-高斯节点、500个单元数量，NE = 15，NP = 5，如图29.3所示中的荷载-位移反应进行计算，可以看出，计算得到的结果和Sloan等（2000年）的结果保持高度一致。

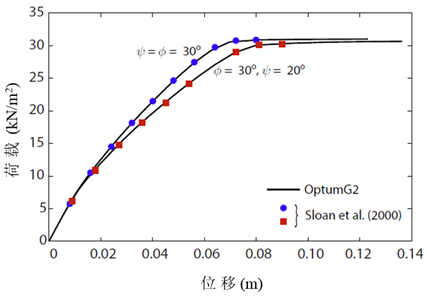
图29.3 条形基础的荷载-位移计算与Sloan等（2000年）的比较

图29.4中显示的是分析结束后的变形和剪切耗散图，可以看到在关联的情况下，Sloan等（2000年）采用的区域大小有点太小，不能被认为是半无限的，尽管这与本分析的结论无关。

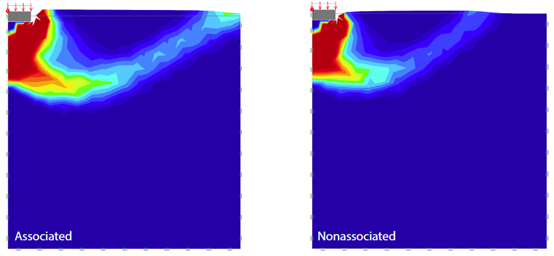
图29.4 变形和剪切耗散图