案例46:一维固结
本案例对OptumG2中的固结分析功能进行了详细介绍。案例如图46.1所示,案例中为一个1m ×1m的弹性材料体,材料的杨氏模量为 30 MPa。为了便于和已知的解析方法(通常规范中采用解析方法)进行结果对比,这里设置材料的泊松比 v = 0。材料体受到 q = 100 kN/m2的荷载作用。

在「工况阶段管理器」界面的「分析」列中选择「固结」即可进行固结分析。相关的固结分析参数则可以在界面的下部进行设置。可其他分析类型一样,首先必须对单元类型和单元数量进行设置。对于本案例,我们选择100个6-节点高斯单元,当然,其他单元类型也是可行的。
参数设置第二栏为「时间步」设置,其中包含了用于控制时间步的各种参数。共有三种不同类型(方案)的时间步:自动,目标/时间,目标/固结度(如图46.2所示)。

「自动」时间步方案在规定步数下自动对时间步进行调整并达到接近完全固结的状态。
对于「目标」时间步方案,可以选择两种不同的目标:时间和固结度。前一种方案需要设置分析终止时达到的时间和达到该时间所采用的步数。后一种方案需要设置分析终止时达到的固结度和达到该固结度所采用的步数。和「自动」时间步方案一样,软件将自动对时间步进行调整。
在OptumG2中,当固结分析没有指定「从」工况阶段时,采用如下分析步骤:
1. 用于确定初始地应力的「初始应力」分析和用于确定渗透压力的「稳定流」分析。这一步和「弹塑性」分析中的流程完全一样,即在进行 K0 分析时,不考虑固定荷载。
2. 在固结开始前先进行「短期」分析,即荷载作用后且超静孔隙水压力开始消散前。这一步和「弹塑性」分析中「时间范围」为「短期」时的分析完全一样。
3. 基于短期分析后的状态,进行长期分析,即计算足够时间长以后的状态。这一步和「弹塑性」分析中「时间范围」为「长期」时的分析完全一样。
4. 开始真正的固结分析。
46.1 固结度
对于一般边值问题,固结度的定义是比较麻烦的,而且在OptumG2中,还提供了多种用于计算短期和长期状态的方法。
首先,根据上述第2步和第3步中计算得到的短期和长期状态,可以得到下述基于功的固结度定义:

其中 W(t) 为时间t时的功,WST 和 WLT 分别为短期和长期时的功。这种定义也许是最一般的测量固结度的方法。但是,问题复杂性在于 WLT 是通过一步计算得到的,而 WLT 和达到长期状态的实际时间过程有关。因此,一步计算可能在一定程度上是不精确的,且固结度 UW 的值可能比实际的固结度更高或更低。
在刚性基础上作用荷载的例子中,基于功的固结度和基于沉降的固结度完全相同:

其中 u(t) 为时间t时基础的竖向沉降,uST 和 uLT 分别为基础的短期和长期沉降。同样的,和其他基于位移的方法一样,这种方法的问题在于最终状态并不是可以事先非常容易的计算得到。
另一我们比较感兴趣的变量是平均归一化超静孔隙水压力:

其中 pe,0(x,y) 是 t = 0 时的孔隙水压力分布(上述第2步中计算得到),pe(x,y,t) 是时间 t 时的孔隙水压力分布。基于该变量,可以得到另一种固结度定义方法:
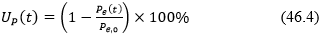
这种方法定义的固结度比基于功定义的固结度UW通常会有一点区别。
在OptumG2中,采用了 UW 和 UP 的组合 U 作为最终的固结度。这种方法得到的固结度通常更接近 UP的值。
结论:固结度在一定程度上是比较模糊的(不明确),所以建议基于计算得到的 U、UW 或 UP 的值,需要仔细判断土体的真实状态。
46.2 解析解
一维固结问题可以采用以超静孔隙水压力为变量的扩散方程形式:

其中固结系数Cv由下式计算得到:

如果固结系数Cv为恒定值,那么可以得到一维固结方程的解析解:

其中H为所分析材料体的高度(在本案例中H=1m)。
得到超静孔隙水压力后,就可以计算得到竖向有效应力和竖向沉降:

46.3 结果
采用「自动」时间步方案,且时间步设置为 20 时得到计算结果如图46.3所示。数值分析结果和解析解结果非常吻合,如果提高时间步的数量,结果的吻合度还可以进一步提升。

图46.3 材料体中心超静孔隙是压力随时间的变化(左)和顶部地表沉降随时间的变化(右)