案例44:采用收敛约束法分析隧道
本案例分析风化岩层中圆形衬砌隧道的开挖过程,如图44.1所示。岩石采用Mohr-Coulomb材料模型模拟,衬砌采用板单元模拟。两种材料的参数如下图所示。
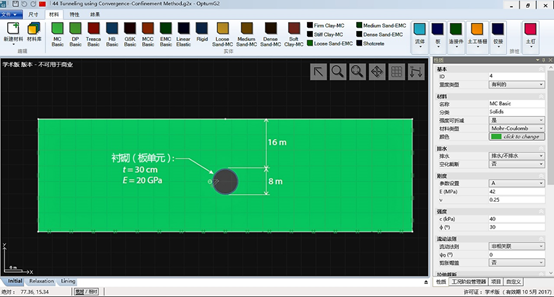
图44.1 圆形隧道
隧道具有很明显的三维效应,最好的方法是采用三维分析。但是,在实践中也发展出了一系列采用平面应变的分析方法,其中包括收敛约束法、逐步软化法、体积损失控制法。Potts和Zdravkovic (2001) 对这三种方法进行了全面的阐述。
所有的平面应变方法均假设隧道断面垂直于开挖方向,关键的问题是应该如何模拟断面的开挖。一种极端情况是先对隧道进行开挖,地应力重分布,然后再施加衬砌。另一种极端情况是先对隧道施加衬砌,然后再进行开挖。对于第一种情况,地表沉降将被高估,而对于第二种情况,衬砌内力将被高估。可以注意到,这两种极端情况都忽略了3D效应 – 第一种情况中假设了一条完全未支护的无限长的隧道,第二种情况中假设了一条提前完全支护的无限长隧道。上述所有的平面应变方法均通过在两种极端情况中找到一个合理的折中方案来考虑3D效应。
接下来,我们采用收敛约束法来进行分析,基本思路如图44.2所示。计算初始地应力后,沿隧道断面边缘整个周长范围内施加「完全支撑」并开挖,这样不会对围岩的应力状态和变形产生影响。然后,逐步松弛(释放)作用在隧道上的围岩压力,即引入松弛系数 α(0 ≤ α ≤1)对支撑进行松弛。最后,施加衬砌并移除隧道断面边缘的所有支撑,这将引起进一步的沉降。
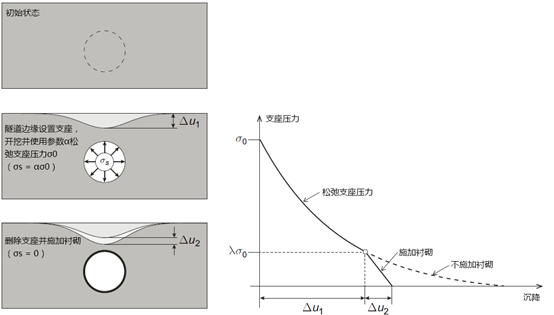
图44.2 收敛约束法示意图(Vermeer et al. 2003)
在OptumG2中,采用收敛约束法分析隧道的步骤如图44.2所示:
1)工况阶段1:采用「初始应力」分析初始地应力。
2)工况阶段2:开挖隧道,且隧道周长范围内设置「完全支撑」并设置松弛系数α,如图44.3所示。
3)工况阶段3:移除支撑,并替换为板单元,用以模拟衬砌。
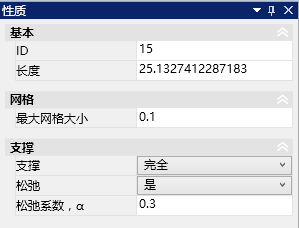
图44.3 OptumG2中的支撑松弛
收敛约法中一个关键的问题是如何选择松弛系数α。在实际工程中,该系数的选取一般基于经验或依据现场试验确定,通常经验值为 α = 0.3或 α = 0.7。较小的松弛系数往往可能高估了地表的沉降,而较大的松弛系数往往可能高估了衬砌的内力。更一般地,为了找到合适的松弛系数值,可以采用一系列可能的松弛系数值分别计算,并建立地表沉降和松弛系数的关系。图44.4和图44.5中给出了隧道中点上方地表沉降和衬砌最大弯矩与松弛系数α的关系。
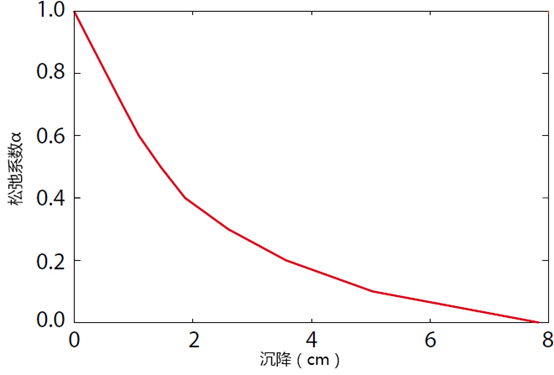
图44.4 地表沉降(Δu1)和支撑松弛系数的关系
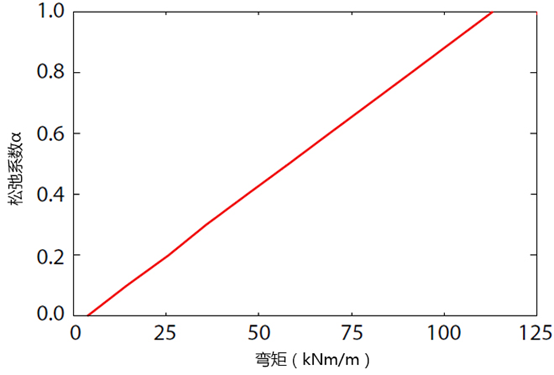
图44.5 最大弯矩和和支撑松弛系数的关系
图44.6给出了取 α = 0.3时,隧道的最终(施加衬砌后)竖向沉降,图44.7给出了衬砌的轴力和弯矩分布。
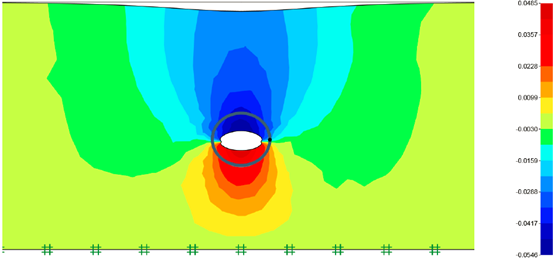
图44.6 α = 0.3时的竖向沉降(变形比列系数取 50)
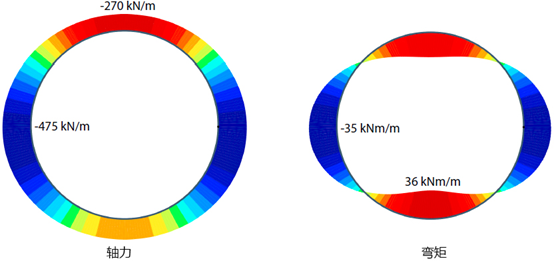
图44.7 α = 0.3时的衬砌轴力和弯矩