4. 孔隙压力:建模与结论
地质力学中的大多数问题都涉及孔隙压力或超静孔隙压力或两者兼有的孔隙压力。尽管上一节中控制方程式已建立完成,但是这些方程式的实际实现可以以多种不同的方式进行。有时单纯是出于方便,有时更多地是由实际物理学驱动的。一些更常见的建模如下:
4.1排水条件及时间范围
原则上,由于负载任何材料都会产生超静孔隙压力。随着时间的流逝,这些超静孔隙压力将消失,即根据达西定律,超静孔隙压力的产生导致的总孔隙压力分布中的不平衡将趋于新的平衡状态。实际上,该平衡状态是由施加载荷之前存在的状态给出的,即具初始超静孔隙压力为0的状态。
对于粗粒状材料,通常认为超静孔隙压力的耗散足够快,始终都可以忽略超静孔隙压力。另一方面,对于细颗粒材料,由于负载,最初会产生超静孔隙压力。然后这些将逐渐消散,以便在足够长的时间后超静孔隙压力再次为零。两种不同的情况如图4.1所示。粗粒材料从不会经历超静孔隙压力累积。这种称之为总是排水。此外,细粒材料在施加载荷后立即承受明显的超静孔隙压力。这些超静孔隙压力会在一段相当长的时间内保持接近其初始值的水平,这种称之为边界是不排水的。足够长的时间后,超静孔隙压力将消失变为排水。
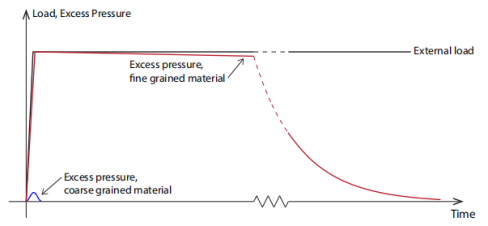
图4.1:粗粒和细粒材料饱和流体对超静压力的响应
在OPTUM G2中,“时间足够长”由两个设置来量化:
时间范围:短期或长期。在管理器里面设置,它指几何结构的加载和/或更改是瞬时发生还是在延长的(原则上无限长)的时间段内发生。一般而言,必须分别针对这两种情况验证地质结构的结构稳定性。例如,在刚放置负载(可能导致产生过大的压力)时和长时间(超静孔隙压力消散时)之后,地基必须稳定。
排水条件:总是排水、排水/不排水、无孔。这是一种材料设置,用于指是否产生了超压。对于总是排水的材料,无论时间范围如何,都不会产生超静孔压。类似砾石、沙子的粗粒材料采用此类材料。对于排水/不排水的材料,对于“时间范围=短期”将产生超静孔隙压力,但对于“时间范围=长期”则不会产生。类似粘土的细粒材料遵循这种模式。最后,对于非多孔材料,既不存在渗透也不存在超静压力(该设置可能与某些类型的岩石,混凝土等有关)。
下表总结了给定的行为是排水还是不排水
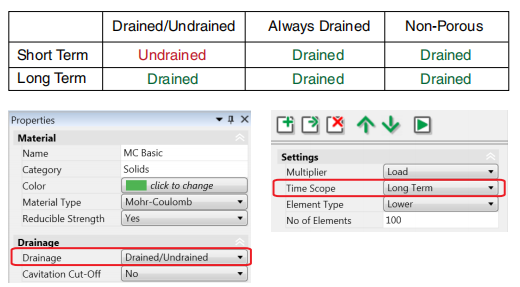
图4.2:材料性能随排水和时间范围的变化而变化
4.2主要变量选择
每当涉及孔隙压力时,总应力和有效应力之间必须进行明显区分。与在分析过程中不存在或不产生孔隙压力的情况相比,平衡方程式保持不变,并且仍包含总应力和总体力。静态边界条件同样不受影响,但应注意,由水压力引起的边界牵引力是总牵引力的一部分(请参见第3.2节)。 真正的区别在于,本构关系涉及有效应力而不是总应力。
这种情况导致至少有三种不同的实现可能性:
1.以总应力表示的平衡和边界条件,以有效应力表示的本构关系以及作为一组约束嵌入的有效应力原理。如3.1中所示。
2.所有控制方程式均根据有效应力和超静孔隙压力确定。如表3.2所示。
3.所有控制方程都是根据总应力和超静的孔隙压力的。
OPTUM G2使用第二种。
4.3不排水总应力分析
在某些特定情况下,可能完全根据总应力进行分析。特别是对于使用Mohr-Coulomb或Drucker-Prager模型进行的不排水分析,在某些情况下可以根据总应力使用不排水材料参数进行分析。与原始排水参数不同但是又与之相关。
例如,考虑线性弹性/完全塑性的Drucker-Prager模型。该模型涉及胡克定律,其参数E和ν 以及屈服和塑性函数:
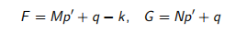 (4.1)
(4.1)
其中M,N和k分别为摩擦系数,膨胀系数和内聚力,p和q分别为平均应力和偏应力(相关详细信息,请参见材料手册)。
4.3.1弹性
假设流体具有可压缩性,则弹性应力-应变关系式为
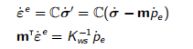 (4.2)
(4.2)
进一步假设渗流压力不变,即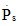 =0。直接假定
=0。直接假定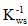 ≈0,应变与总应力之间的关系将如下:
≈0,应变与总应力之间的关系将如下:
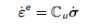 (4.3)
(4.3)
其中
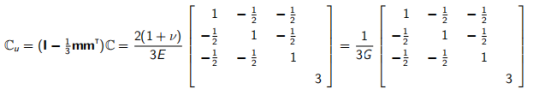
换言之,就应变与总应力而言,其弹性行为与杨氏模量Eu = 3E / 2(1 +ν)且泊松比νu= 1/2的排水材料的相同。可以认为它的剪切模量G不变,泊松比νu= 1/2。或者可以利用(4.2)根据有效应力和超静孔隙压力进行建模,或者利用(4.3)根据总应力进行建模。在这两种情况下,我们都有
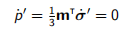 (4.4)
(4.4)
也就是说,有效平均应力始终保持其初始值。
4.3.2塑性
由于介质的不可压缩性,体应变变化为零。屈服前,弹性体应变的变化为零,而屈服时,弹性和塑性体应变的总和为零:
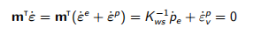 (4.5)
(4.5)
其中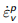 是塑性体应变变化率:
是塑性体应变变化率:
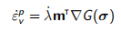 (4.6)
(4.6)
因此,超静孔隙压力的变化如下式:
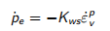 (4.7)
(4.7)
注意Kws非常大,任何小的塑性体应变都会导致超静压力显著降低。总平均应力恒定,有效平均应力的减小会有效地提高了剪切强度。对于典型的弹塑性分析,这意味着将永远无法达到极限载荷。极端情况下,依据塑性势(plastic potentia),塑性应变速率为零。此时,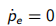 屈服,有效平均应力保持在其初始值。
屈服,有效平均应力保持在其初始值。
因此,对于Drucker-Prager准则,我们可以得出结论,应该使用N = 0的膨胀参数来使结果有意义。此外,由于有效平均应力永远不会从其初始值发生变化,因此屈服函数可以写为:
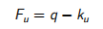 (4.8)
(4.8)
其中 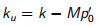 是有效“排水强度”参数。
是有效“排水强度”参数。
总而言之,可以使用以下等式根据总应力进行不排水的弹塑性分析:
弹性 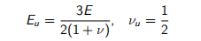
塑性 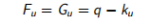 (4.9)
(4.9)
4.3.3 Mohr-Coulomb
针对Mohr-Coulomb准则进行与上述相同的分析,得出以下不排水方程:
弹性 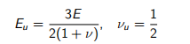
塑性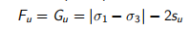 (4.10)
(4.10)
屈服力和塑性势(plastic potentials)这里用带有强度参数的Tresca函数:
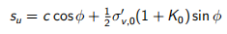 (4.11)
(4.11)
其中c和ϕ是在排水条件下测得的Mohr-Coulomb参数,K0是初始土压力系数,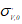 是初始有效垂直应力(压为正)。
是初始有效垂直应力(压为正)。
参数su被称为不排水剪切强度。如上所示,它是排水参数和初始应力状态的函数。但实践中可以考虑su空间分布,该分布与现场测量的结果更接近。在OPTUM G2中,Tresca模型可做此考虑。