案例33：砂土中锚杆的抗拔分析

本案例对砂土中的锚杆进行抗拔分析，如图33.1所示。岩土材料采用软件自带的「松散砂土-MC」，锚杆采用无重度的刚性板模拟，且和土体之间的接触考虑为完全粗糙。模型左右对称，因此取模型的一半进行分析，图33.1中模型相对于左边界对称。我们再次使用「乘数弹塑性」研究流动法则的影响，即：关联流动法则（ψ = φ）和非关联流动法则（ψ = 0）。在这两种情况中，土体黏聚力均为零。

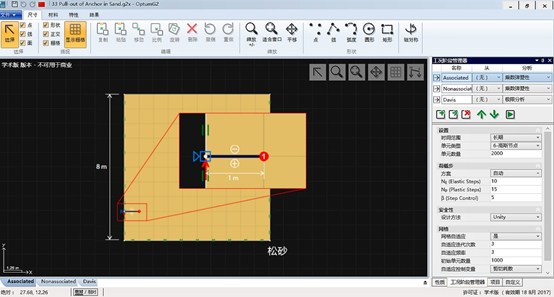
图33.1 松散砂土中的锚杆抗拔分析

关联流动法则和非关联流动法则分析采用的工况阶段设置如图33.1所示。和前面的案例相比，这里我们采用较大于「弹性」步数目（NE = 10）的「塑性」步数目（NP = 15）。同时，网格自适应采用默认设置，即「自适应迭代次数 = 3」和「自适应频率 = 3」。

最终计算得到的荷载-位移曲线如图33.2所示。和前面案例中分析得到的结论一样，非关联性意味着土体强度和刚度在一定程度上的折减。但是，和前面的案例相比，本案例中的Davis摩擦角 φ_D = 26.5650°，略大于非关联情况下的内摩擦角，这一点已经被Krabbenhoft et al. (2012) 提出并讨论过。目前的结果进一步证明了虽然Davis参数通常可以很好的估算非关联材料的强度，但是并不总是偏保守的。

最后，图33.3中给出了分析结束后得到的土体变形和塑性乘数云图。和前面的案例一样，可以看到剪胀角对结果的影响是很明显的。

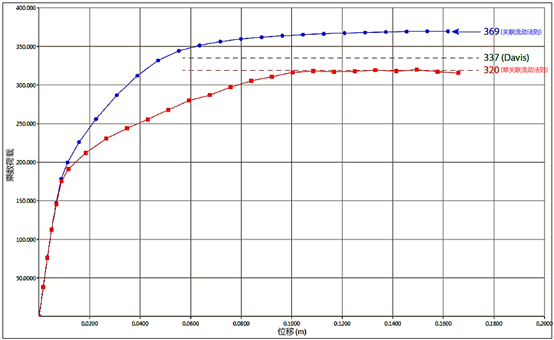
图33.2 锚杆拔出松散砂土过程的荷载-位移曲线

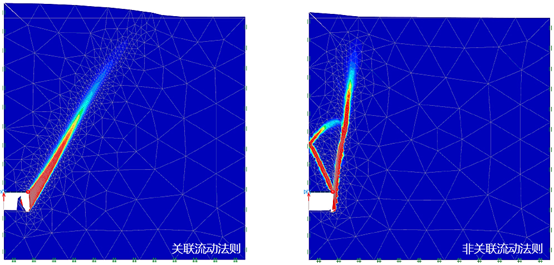
图33.3 变形（比例系数为 5）和塑性乘数云图