案例9：水位骤降时边坡的稳定性

本案例中分析水位骤降对边坡稳定性的影响。分析模型设置如图9.1中所示。从下图中所示的初始状态开始，水位突然下降。由于下游水位对边坡稳定有利，随着水位下降，边坡稳定性安全系数也将下降。

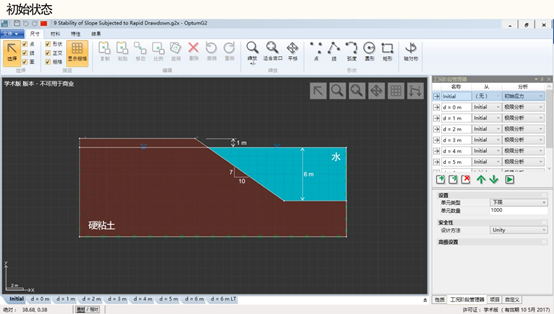
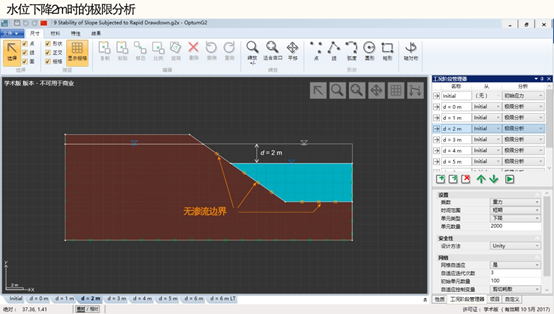
图9.1 水位骤降时边坡的稳定性

由于水位骤降，土体内的渗流场将根据新的水利边界条件而变化。同时，由于应力场也发生了变化，将产生超静孔隙水压力。

9.1 短期稳定性

首先，分析边坡的短期稳定性，即假设坡体内的渗透压力和初始状态相比没有任何变化。另一方面，大坝前的库水中，假设始终作用有静水压力。考虑到材料的渗透性很差，该假设是合理的。和其他类似的分析一样，当「时间范围」设置为「短期」，且材料排水条件为「排水/不排水」时，计算中将自动产生超静孔隙水压力。

图9.2 水位骤降前（左）和水位骤降2m后（右）的渗透压力（kPa）

采用下述方法分析边坡的短期稳定性。首先，在「初始应力」工况阶段采用「初始应力」分析边坡的初始地应力和初始渗流场（如图9.2所示）。然后，新建一个「极限分析」工况阶段，并设置相应的大坝水位骤降深度。在该工况阶段中，将「初始应力」工况阶段作为「从」工况阶段，且「时间范围」设置为「短期」。另外，在坡面和库底上设置「没有渗流」边界条件，从而保证坡体内和库水中的渗透压力均可以达到静水压力状态（如图9.2所示）。

接下来，设置极限分析的「乘数」为「重力」，即得到的安全系数是基于增大边坡重力的方法。采用2000个网格单元，3次网格自适应，分别进行下限和上限分析，分别分析不同骤降深度下边坡的稳定性安全系数，如图9.3所示。可以看到，安全系数随骤降深度的增大而减小。图9.4中分别给出了骤降深度为 d = 0m和 d = 5m时的边坡破坏模式。

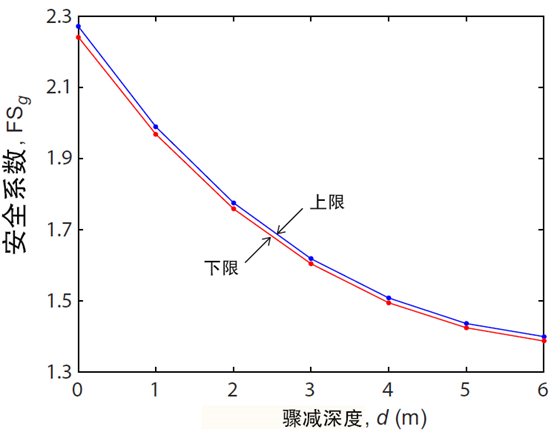
图9.3 基于重力增大重力的安全系数上限和下限解，FSg

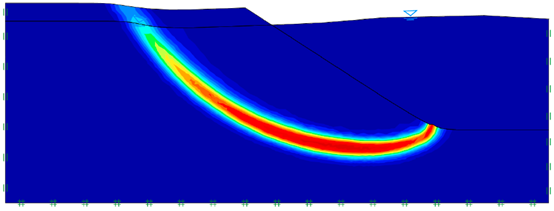
图9.4 水位骤降前（上）和水位骤降5m后（下）增大重力极限分析得到的边坡破坏模式

9.2 长期稳定性

最后，对水位下降到最大深度d = 6m后的长期稳定性进行分析。首先删除坡面和库底上的「没有渗流」边界条件，同时设置「时间范围」为「长期」，此时极限分析前将首先对水位下降后的情况进行稳定流分析，以得到长期状态下坡体内的稳定渗流场。使用和短期稳定性分析相同的网格单元数量和网格自适应参数，得到如下结果：

FS_g = 2.07 ± 0.06                （9.1）

图9.5中给出了孔隙水压力分布和边坡的破坏模式。

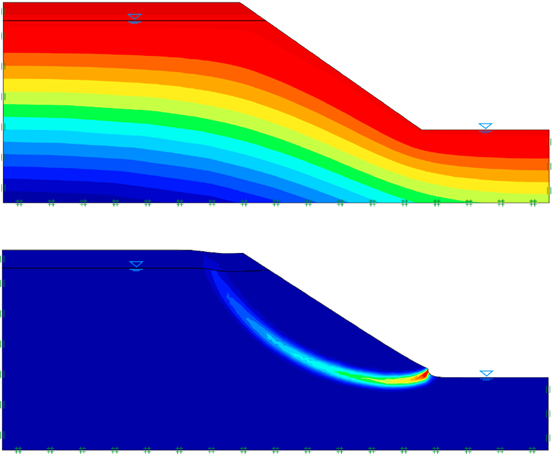
图9.5 水位骤降6m后长期状态下的孔隙水压力分布（上）和破坏模式（下）