案例56：砂土中环形锚杆的抗拔能力分析

下面的示例是受到Dyson和Rognon（2014）的研究启发而做的，他们通过形似于树根的分形几何制造并测试了锚板，图56.1显示的是Dyson和Rognon采用的一些锚板示例。值得注意的是，抗拔能力受板面积的影响相对较小，也就是说，图56.1中右边的板的抗拔能力与左边显示的标准圆板相差无几。

图56.1 标准的圆形和分形锚板（Dyson和Rognon（2014）之后）

如图56.2所示，模拟的是一个环形锚杆的抗拔能力。在实践中，显然需要一个系统将力从中心传递到环（例如图56.2所示的辐条的形式），在下图中，这个系统被隐藏了，只在图中显示了轴对称模型中的环。注意，连接件是用来向锚杆施加力的作用的。虽然这种设定在这种情况下不是绝对必要的（可以直接在锚杆上施加一个力），但它可以适用于包含多个同心环的环孔锚杆。

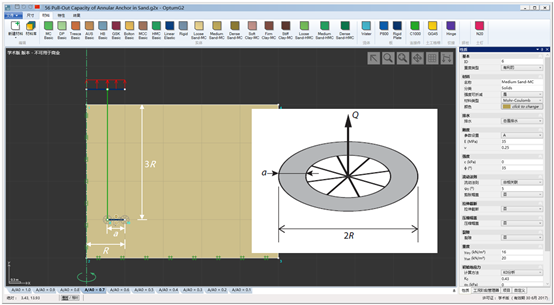
图56.2 环孔锚杆

土体是用软件默认的「中砂-MC」来模拟，分析方法采用的是极限分析，上限和下限解网格划分数量是5000，自适应迭代次数为3次。如图56.3所示的是锚杆之间的相互作用力与相对锚板面积之间的关系，轴上的参数有：

        Q₀ = 全局圆型锚板的拉应力（a＝R）；

        Q = 环形锚板的拉应力，宽0 < a < R；

        A₀ = 全局圆形锚板的面积 ＝πR²；

        A = 环孔的面积=π[R² - ( R – a )²]；

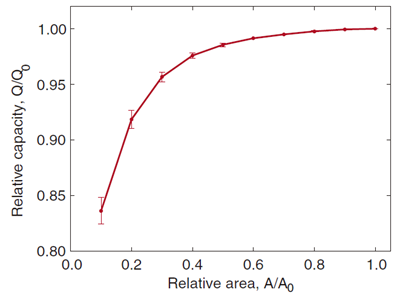
图56.3 相对抗拔能力与相对面积的关系曲线

可以发现，锚板的面积对抗拔能力的影响非常小，将面积减小一半，只起到很微小的作用；将面积减小10倍，拉应力减少20%。这些结果也验证了Dyson和Rognon（2014）的试验结果。

图56.4显示了选择的不同A/A₀所对应的破坏机制，这些反映了图56.3所示的承载能力，也就是说，通过减小环孔面积产生的影响效果非常有限。

图56.4 A/A₀ = 0.1、0.5和1所对应的破坏机制