03 弹塑性

OptumG2在本构模型的制定中广泛使用弹性塑性理论。 在诸如三轴压缩试验的标准实验室测试中，这些模型意味着在低负载水平下的初始弹性响应。其次是塑性或不可逆应变的积累，直到应力水平向稳定状态渐近渐近，或者在某些情况下下降到较低水平。弹塑性材料的典型应力应变响应如图3.1所示。

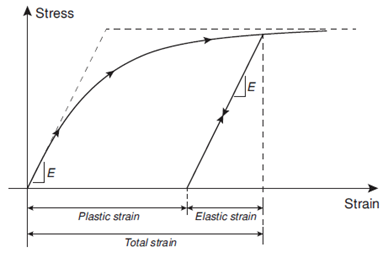
图3.1 弹塑性材料的应力-应变曲线

下面，将简单的介绍弹塑性理论，关于OptumG2中更多类型的材料将会详细讲解。

3.1 加成与分解

弹塑性理论的基本假设是弹性应变和塑性应变的加成与分解（如图3.1所示）：

                                                                ε = ε^e + ε^p                                                                 (3.1)

其中，ε 是总应变，ε^e 是弹性应变，ε^p 是塑性应变。

3.2 弹性

假设为线弹性，弹性应变与有效应力的关系可通过虎克定律确定：

                                                     ε^e = Cσ'   ←→    σ' =  Dε^e                                                   (3.2)

其中，C是柔度模量，D是刚度模量（见第2节），此定律常以增量形式表述，但也适用于有效应力和弹性应变的总和。

3.3 流动法则

塑性应变与应力的关系通常通过下式的流动法则来表示：

                                                                                                                               (3.3)

其中，G是流量， 是一个标量（即所谓的塑料乘数），上方的圆点表示增量。

3.4 屈服函数

应力受屈服函数的限制，这通常是类似应力硬化的函数，但也可能涉及各种额外的变量，因此屈服函数可用下式来表示：

                                                                   F（σ' , k）                                                              (3.4)

其中，σ' 是有效应力，k 是类似应力的变量。对于屈服函数 F<0 时，对应的是纯弹性状态；当 F＝0 时则表示屈服状态，在任何情况下都不允许出现 F> 0 的状态。虽然许多模型只使用一个屈服函数，但原则上可以把任意数合并到一个模型中。

3.5 硬化规则

硬化变量k的演化是通过硬化规则来确定的，通常可以用下式来表示：

                                                                                                                          (3.5)

其中，h是硬化函数。

3.6 补充条件

塑性乘数  必须是非零的，只对应于屈服的应力状态，这一要求可以通过互补条件来表示：

                                                                               (3.6)