案例11：地震作用下的边坡稳定性

岩土结构在地震作用下的稳定性通常采用拟静力法进行分析。地震荷载引起的地震力采用体加速度来模拟，将地震荷载考虑为一个静态体力。通常，分析方法为保持竖向加速度不变g_v = 9.8 m/s²（重力加速度），水平加速度逐渐增大，直到破坏。最终得到的竖向加速度和水平加速度之比 k_c = g_h/g_v即为临界地震加速度系数。本章中，我们对图11.1中的边坡进行分析。

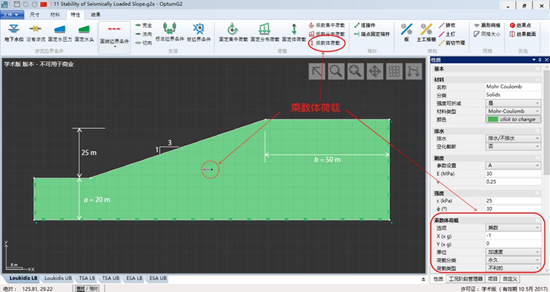
图11.1 地震作用下的边坡

拟静力地震荷载采用乘数体荷载模拟。乘数体荷载只能添加到实体或结构单元上，选择相应的实体或结构单元后，在「特性」界面中点击「乘数体荷载」即可。体荷载可以采用两种不同的单位输入：按力输入（kN/m³）或按加速度输入（即默认重力加速度 g = 9.8m/s² 的倍数）。在本案例中，采用第二种方式输入。采用「极限分析」且设置「乘数」为「荷载」，则计算得到的破坏乘数即为临界地震加速度系数 k_c = g_h/g_v。

11.1 Loukidis et al.案例

我们首先分析一个典型的案例，Loukidis et al. (2003) 曾对该案例进行过分析。材料采用Mohr-Coulomb模型，c = 20 kPa，φ = 30°，重度为20 kN/m³。采用「极限分析」，网格单元数量为1000，网格自适应次数为3。边坡体不产生超静孔隙水压力，因此「时间范围」设置为「长期」，虽然地震力显然是短期作用力。基于以上分析参数，我们得到：

0.427 ≤ k_c ≤ 0.439             （11.1）

该计算结果和Loukidis et al. (2003) 采用4种不同的方法（Spencer法、Bishop法、Sarma法、对数螺旋上限法）手算得到的临界地震加速度系数范围（0.426 ≤ k_c ≤ 0.432）基本一致。另外，Loukidis et al.还采用传统的有限元方法进行了计算，得到的结果为 k_c = 0.433。OptumG2采用极限分析计算得到的临界地震加速度系数的范围和目前采用其他方法得到结果基本接近。

11.2 短期条件 – 总应力法分析

接下来，我们考虑边坡短期状态下的地震作用。和其他岩土工程问题（基础、边坡等）的分析类似，总应力分析通常采用Tresca模型（单一强度参数 – 不排水抗剪强度）替换Mohr-Coulomb模型。如果数据有限，那么可以采用恒定的不排水抗剪强度值。为了得到合理的结果，该值建议采用整个坡体内不排水抗剪的平均值。但是，该方法有时并不正确，且会导致不合理的结果，如下文所述。

模型尺寸和图11.1中的一样，除了尺寸参数a和b是变化的。材料采用Tresca模型，且不排水抗剪强度为s_u = 150 kPa。在11.1的案例中，当尺寸参数a和b足够大时，临界地震加速度系数和参数a、b无关。但是，如果只考虑材料的黏聚力（不排水抗剪强度），那么临界地震加速度系数则和参数a、b直接相关。图11.2中，在保持 a/b = 2.5 的比例不变的情况下，逐渐增大a和b，可以看到无论边坡的尺寸多大，破坏面总是交于模型的右边界和底边界，且尺寸越大临界地震加速度系数越小，并逐渐趋近于零。

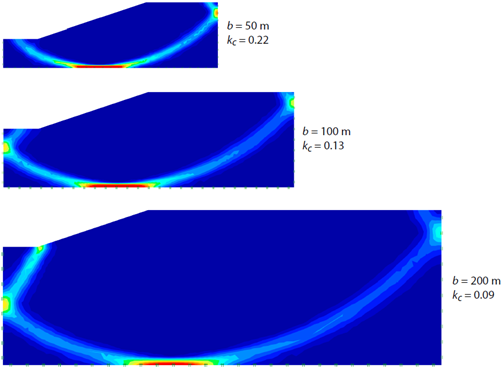
图11.2 不排水抗剪强度为恒定值时边坡尺寸变化对破坏面的影响

11.3 短期条件 – 有效应力法分析

采用随深度增大的不排水抗剪强度，或采用有效应力法分析，可以得到更加合理的计算结果，其分析参数为：「时间范围」设置为「短期」，材料排水条件设置为「排水/不排水」。如果没有指定「从」工况阶段，那么软件将采用土压力系数K0（K0法）自动计算初始地应力状态。

采用软件自带的「硬塑黏土-MC」材料和上述中的分析设置，得到

0.183 ≤ k_c ≤ 0.188        （11.2）

破坏模式如图11.3所示。

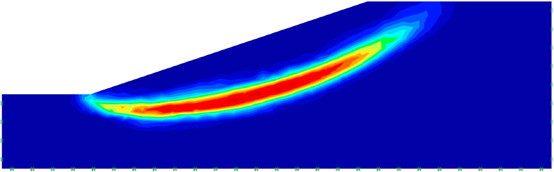
图11.3 硬塑黏土-MC边坡短期状态下的破坏模式