12 随机分析

通常认为与设计相关的典型土壤参数空间变化不明显。在传统设计中，这是在空间上使用独立“谨慎估计”的相关参数的来解决。例如，如果已在多个不同位置测量了给定参数，则可以通过使用偏向于所测量参数范围的不利端的加权平均值来确定最终值。

作为传统确定性分析的替代方法，OPTUM G2提供了进行随机分析的可能性。 这里分析可以考虑空间可变性，从而不仅获得了承载力、沉降、强度折减系数等值，而且还获得了它们的概率分布。

在OPTUM G2中，可以通过为特定参数生成随机字段并随后通过一系列蒙特卡洛模拟运行分析来考虑参数的空间变化。 最终结果是分析关键结果的概率分布，例如承载力（极限分析），沉降（弹塑性分析）或强度折减系数（强度折减分析）。

12.1 OPTUM G2输入

要生成给定材料参数的随机字段，需要四个输入参数：

1.参数的平均值（图12.1中的30 kPa）。 可以使用梯度，剖面和图来指定参数平均值的空间分布。

2.参数变异系数（图12.1中的35％）。

3.参数的水平相关长度（图12.1中的50 m）。

4.垂直相关长度（图12.1中的1 m）。

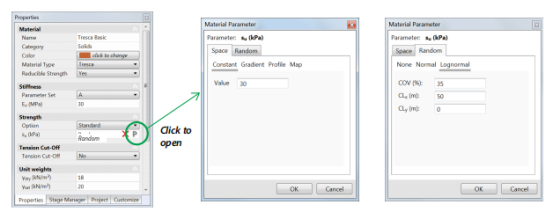
图12.1：用于随机分析的参数规范。平均值（或平均值的空间分布）在“空间”选项卡中指定（中间），其余参数在“随机”选项卡中指定（右侧）

相对于潜在的概率密度函数（正常或对数正态）指定参数。

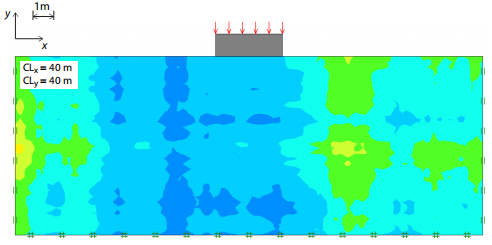
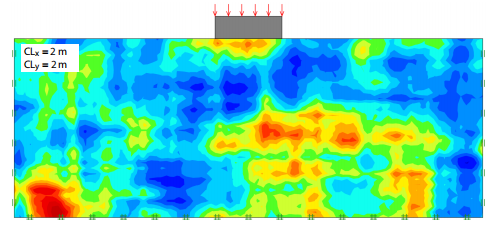
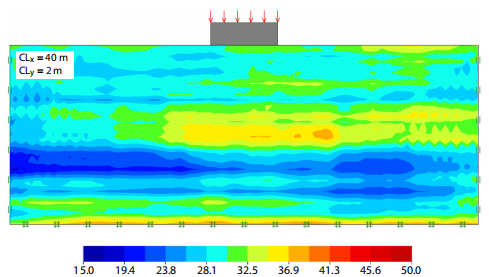
图12.2：不排水抗剪强度随机场的示例。所有案例，平均值和变异系数分别为30 kPa和30％。

空间相关长度描述了空间随机值将趋于明显相关的距离。 因此，较大的值将表示平滑变化的场，而较小的值将表示较粗糙的场。图12.2中显示了一些示例。 通常假定岩石和土壤的所有工程特性的空间相关结构是相同的。 也就是假设摩擦角与杨氏模量的相关结构相同。 通常认为水平相关长度比垂直相关长度大。 Phoon and Kulhawy（1999）进行了文献综述，得出的结论是，水平相关长度在40-60 m量级，而垂直相关长度在2-6 m范围内。

除物理参数外，还提供与随机分析有关的其他参数

在随机参数下的项目中。 这些包括：

•蒙特卡洛运行次数（默认= 1,000）。

•用于生成随机字段的种子。 每次新的蒙特卡洛运行，种子将增加1。 因此，为了恢复蒙特卡洛模拟中第n次运行的问题，可以将种子设置为n并执行一次蒙特卡洛运行。

12.2 OPTUM G2输出

随机分析的输出是取决于分析类型的各种关注量的概率密度和累积密度函数。对于极限分析，记录破坏乘数，对于强度减少分析，记录强度折减系数，而对于弹塑性分析，记录关键数值，如结果点的位移。此外，如上所述，要恢复第n个蒙特卡洛运行的完整解，应将种子（“项目/随机参数”）设置为n并执行一次蒙特卡洛运行。

如果需要比默认情况下更多的信息，则该程序的命令行版本OPTUM G2Cmd很有用。首先可以生成所需数量的输入文件，每个文件具有不同的种子，并设置为执行单个蒙特卡洛运行。然后可以使用OPTUM G2Cmd运行它们，并通过外部脚本进一步处理结果。

12.3随机场理论

以下部分简要概述了随机字段的概念以及这些字段的生成。

令X（x，ω）为随机字段，其中x∈D定义物理空间，而ω∈Ω定义概率空间。 随机字段的相关结构由协方差函数建模，用CX（s，t）表示，其中s，t∈D是有界的，对称的并且是正向定义的。

随机场理论应用中的第一个问题是选择场的概率分布。尽管可以使用许多概率分布，但对数正态分布具有一些明显的优势，通常用于对土壤和岩石的工程特性进行建模。对数正态分布的优点是简单，因为它是通过经典正态高斯分布的简单非线性变换得出的。此外，对数正态分布确保随机变量始终为正。

其次，关于协方差函数，存在多种可能性（例如Fenton和Griffifiths 2008），而指数协方差函数通常是选择函数。除均值和标准差外，协方差函数还涉及空间相关长度。

12.3.1 Karhunen-Loeve展开

几种随机场生成方法可供使用（例如参见Fenton和Griffifiths 2008）。 在OPTUM G2中，使用了Karhunen-Loeve展开方法。 这种方法很方便，因为它提供了指数协方差函数的解析解。使用Mercer定理，可以根据以下公式分解协方差函数

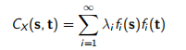(12.1)

其中λi和fi分别是CX的特征值和特征函数。

由于必须将上述总和截断为有限数量的项，因此，一个重要的问题是将减少模拟方差。为了控制这种减少，特征值按降序排列，项数n由充分衰减以满足条件的特征值决定

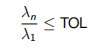(12.2)

其中 TOL通常设置为 10^-5.

12.4风险

在OPTUM G2中可能进行的大多数随机分析的目的是确定破坏概率或沉降超过一定幅度或类似的概率。此外，还确定了全概率密度函数，从而提供有关问题敏感性的有价值的信息。

风险的概念不仅考虑特定事件（例如破坏）的可能性，还将这种类型的分析更进一步，还可以量化此类事件的后果。某事件的后果显然是高度依赖问题本身的，一般度量通常是与破坏相关的是滑动的土壤的体积。这对于边坡稳定性特别重要，在该边坡中，较深的失稳通常意味着较严重的后果。因此，在OPTUM G2中，记录了每次蒙特卡洛运行中滑动的土壤量。继黄等。 （2013），则可以将风险R定义为

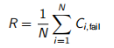(12.3)

Ci，fail是第i次的滑动的土壤量—假设此运动暗示破坏，否则Ci，fail = 0。

在OPTUM G2中，通常将使用强度折减或重力乘数的极限分析来进行边坡稳定性分析。在这两种情况下，强度折减系数/破坏乘数均小于1表示发生破坏，而值大于1则表示系统稳定。 由于记录了所有运行的滑动的土壤量，要根据上述方法计算风险，必须进行手动筛选。