7 弹性

线弹性和非线弹性边值问题的变分原理应用已久，并且经常被用作有限元近似的基础。

在下文中，提出了许多这样的原理。

7.1控制方程

控制方程包括：

平衡和静态边界条件：

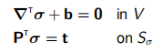(7.1)

应变位移相容性：

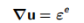(7.2)

本构准则：

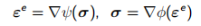 (7.3)

其中∇ψ和∇ϕ分别是Helmholtz free和能量守恒原理。假定这些函数是凸函数，并且满足

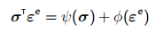 （7.4）

因此，对于线弹性，其中C和D分别是弹性柔度模量和刚度模量。 而且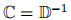，我们有

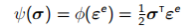(7.5)

7.2能量守恒原理

可以证明控制方程（7.1）-（7.3）可优化为：

最大化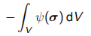

满足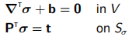 (7.6)

该原理被称为总能量守恒原理，可以看作是弹性模拟下限原理（6.16）。 即仅在应力作用下，在解决问题的过程中也可以考虑位移，称为平衡约束相关联的拉格朗日乘数。

7.3势能原理

或根据总势能原理来转换控制方程式：

最小值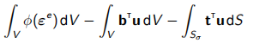 

满足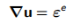                (7.7)

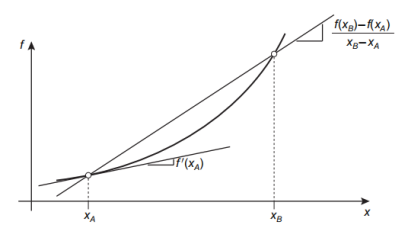
图7.1：凸函数

这种形式与上限原理（6.17）有相似之处。是最常用的有限元法的基础形式。

7.4 Hellinger-Reissner原理

最后，Hellinger-Reissner原理通常可用于构造非标准的有限元公式。该原理

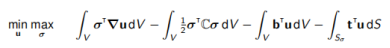(7.8)

通过位移的目标函数最小化并且相对于应力使目标函数最大化来再现控制方程。

7.5界限

原理（7.6）和（7.7）提供了系统能量的界限。此属性可用于计算研究属性的上限和下限，或者用作衡量近似解与精确解的接近度的一种方法。

凸函数f（x）是该函数位于其所有切线之上的函数：

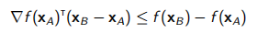(7.9)

对于所有xA和xB（请参见图7.1）。

考虑到（7.6），任何可接受的（并不一定是最佳的）应力分布σa都满足虚功原理：

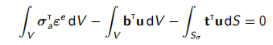(7.10)

其中u是精确位移场，εe=∇u。 同样，精确的应力分布σ满足：

(7.11)

从（7.10）中减去（7.11）并联合（7.3）和（7.9）得到

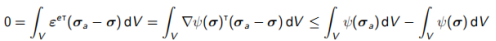(7.12)

或：

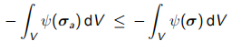(7.13)

上述证明了（7.6）的下限性质。 一般而言，我们可以说由于内部能量被高估了，因此外部能量也是，对于固定负载，虚功原理所隐含的位移要大于精确位移。回到（7.7），我们考虑了容许位移场的虚功原理以及精确应力：

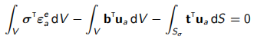(7.14)

精确的位移和精确的应力：

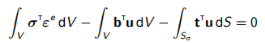(7.15)

从（7.14）中减去（7.15）并联合（7.3）得到

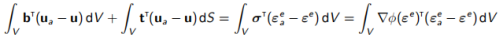(7.16)

使用 (7.9)，得到 

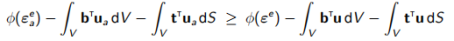(7.17)

上述证明了（7.7）的下限性质。这种不等式意味着，就给定的一组外力而言，位移被低估了，从某种意义上讲，近似的解决方案一般来说“太僵硬”。 这是基于最小势能原理的标准位移有限元方法的众所周知的特性。

7.6耦合

最后，证明问题（7.6）和（7.7）是相互耦合的，因为相同的数据和相同的解决方案。我们考虑两个允许但不一定相关的变量ua和σb。（7.7）目标函数减去（7.6）目标函数，得出

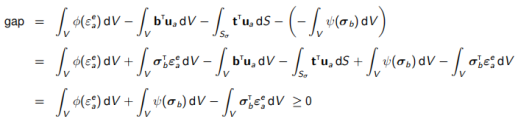
其中最终的不等式来自于上一节。我们看到，当位移和应力均为精确场时，gap差值消失。