案例30:MC粘土中基础的荷载-位移分析
本案例主要介绍了浅基础的荷载-位移分析,如图30.1所示。土体采用的是默认的硬黏土材料,基础采用刚性材料来模拟,重度为22kN/m3。分析方法采用的是乘数弹塑性分析,分析时乘数逐渐递增,直到达到承载能力或者达到指定的荷载水平或位移(详细信息见前一节)。土体和基础的接触面采用剪切节理模拟,材料采用用来模拟土体的硬黏土,但是强度需要进行折减,cinterface = 0.5×csoil = 5 kPa,φinterface = arctan[0.5tan(φsoil)] = 10.3°。
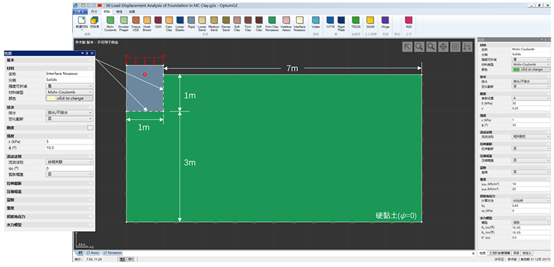
图30.1 硬黏土中的浅基础
弹性参数
对于乘数弹塑性分析,与目前讨论的大多数问题不同,必须同时考虑弹性参数和塑性参数。弹性参数可通过两种方式定义:一种是参数设置A,包括杨氏模量E和泊松比v,还有一种是参数设置B,包括体积弹性模量K和剪切模量G,关于这两种参数设置的关系可参考材料手册。软件默认采用的是参数设置A。需要注意的是,这两种设置相互之间是不关联的,即对其中一种设置进行更改不会影响另一设置中的参数。
流动法则
在之前涉及到极限分析和强度折减分析的案例中,假定流动法则都是相关联的。事实上,极限分析的框架非常关键地取决于这种流动法则。然而众所周知的是,实际上关联流动法则倾向于高估典型材料的膨胀性。与极限分析相反,乘数弹塑性分析打开了使用任意流动法则的可能性。对于Mohr Coulomb准则,流动法则是通过剪胀角ψ来指定的,如材料手册中所述。总之,ψ=φ意味着是关联流动(对于大多数材料,即过度膨胀),而ψ= 0意味着塑性应变体积为0。在不排水条件下,相关联流动法则则会出现问题,它会导致出现一个无限的极限荷载,任何剪胀角都大于零。
乘数弹塑性分析设置
乘数弹塑性设置是默认的,由于没有指定“从”工况,软件会采用初始应力分析自动计算初始应力。初始应力分析的目的是能够找到一个满足屈服和平衡条件的应力状态,最大程度上满足初始应力条件![]() (详见分析手册)。在本案例中,土压力系数K0 = 0.66。
(详见分析手册)。在本案例中,土压力系数K0 = 0.66。
30.1 短期分析
首先进行短期分析,荷载步的所有参数均采用默认设置参数,乘数弹塑性分析的默认单位类型是6-高斯节点,单元数量为2000。
求解后,可以采用与先前的分析类型同样的方法对最终状态的应力、应变、位移等的分布进行绘制。
此外,结果点位置的各种数据会被保存下来,之后可以通过结果栏计算书里面的XY绘图工具进行绘制(如图30.2所示)。
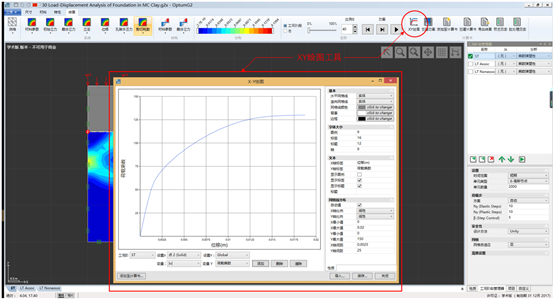
图30.2 短期分析中采用XY绘图工具绘制的荷载-位移曲线
进入XY绘图工具窗口,首先选择需要绘制结果的工况,然后选择多个结果集当中中的一个,最后使用添加按钮绘制结果集中的变量。对于X轴,设置X选择之前定义的结果点1(实体),从当中选择变量|u|(位移长度,|u| =![]() ),这是在这种情况下的垂直位移的绝对值。对于Y轴,设置Y选择General,从当中选择荷载乘数,生成的曲线显示了基础位移(向下为正)与荷载乘数之间的关系,因为参考乘数分布荷载为1,所以荷载乘数等于荷载q(kN/m2)。
),这是在这种情况下的垂直位移的绝对值。对于Y轴,设置Y选择General,从当中选择荷载乘数,生成的曲线显示了基础位移(向下为正)与荷载乘数之间的关系,因为参考乘数分布荷载为1,所以荷载乘数等于荷载q(kN/m2)。
最终状态的变形和非关联材料的剪切耗散分布如图30.3所示,破坏区域与剪胀角ψ=0一致。

图30.3 最终状态的变形(缩放系数为10)和剪切耗散分布分析
在上述分析中采用极限分析法计算出了最终的极限荷载,上限解和下限解分别采用上下单元来计算。此外,这些单元可用于乘数弹塑性分析,不仅包括极限强度,也包括系统的刚度。如图30.4所示,所有分析都采用了2000个单元。
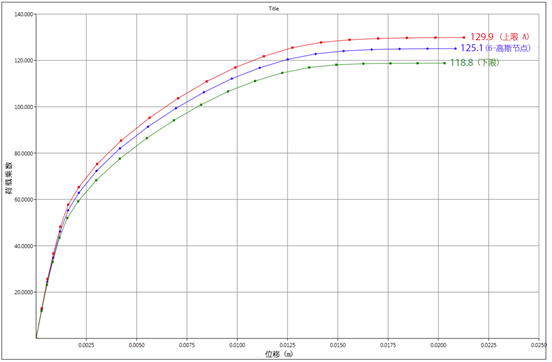
图30.4 采用6-高斯节点的短期乘数弹塑性分析,上下限解
30.2 长期分析
在长期分析中考虑两种情况:ψ=φ和ψ= 0,进行长期分析非常容易,只需要将时间范围更改为长期即可(在工况管理器中进行设置)。
对于计算,应该指出的是,关联材料的计算在每个荷载步只需要一个单一的解决方案,而非关联分析在每个荷载步需要一定的迭代次数,每一次迭代约等同于一个单一的相关联计算。因此,非关联材料分析通常比同等的关联计算更繁琐。在本案例中,相比于关联分析每个荷载步需要单一的解决方案,非关联分析每个荷载步平均需要3个解决方案。
计算得到的荷载-位移曲线如图30.5所示。在这种情况下,承载力的差异是相对变小的,而在某些特定荷载水平上的位移差异却更为明显。在相关联方面,非关联材料是比较保守的,即相比同等的关联材料硬度更低、强度也更小。同时可以说明,关联材料的强度总是大于或等于非关联材料,但是变形可能有所不同:对于一些问题(例如当前的问题),关联流动法则意味着更小的位移,而其他问题的趋势是相反的。同时可以看出,在非关联的情况下荷载-位移曲线出现明显的软化,这是流动法则本身的原因,而不是数值软件或材料软化的结果(详见理论手册)。
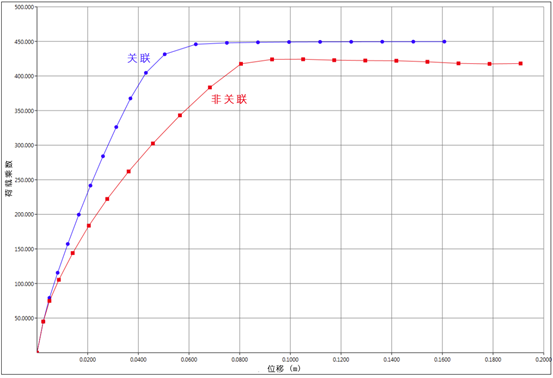
图30.5 长期分析的荷载-位移曲线
两种情况下的变形和塑性乘数场如图30.6所示,可以看到两者的破坏模式和剪胀角都是有所不同的(例如,在关联材料的垂直土体-基础界面上)。此外,关联材料的塑性应变(由塑性乘数场测量)更具局部性。
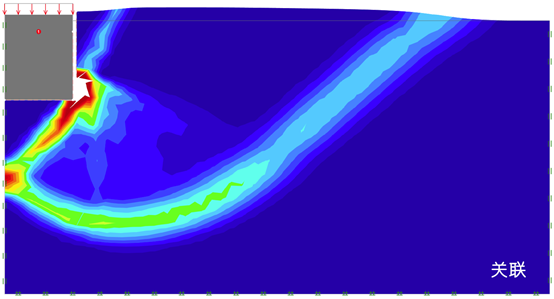
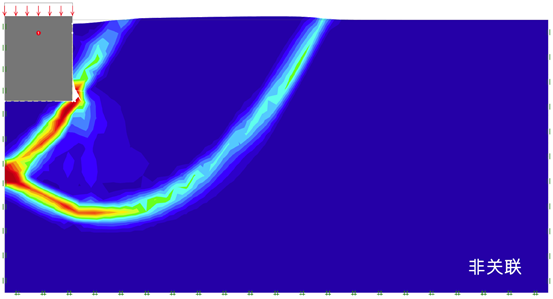
图30.6 最终状态的变形(按规定比例)和塑性乘数场分析
30.3 极限分析
对上述类型弹塑性分析的极限分析主要优点是确定极限荷载只需要一个单一的计算,缺点是无法得到关于位移的信息(除了破坏机制)。此外,极限分析的一个关键特征是流动法则为相关联,在短期分析中,这基本上意味着极限载荷是无穷大的。然而,在OptumG2中采用的是更加专业的极限分析,能够考虑在不排水条件下的零剪胀角。因此,根据极限分析中使用的单元类型,将得到与上述结果相似或相同的结果,在排水条件下,极限分析的流动法则总是关联的,这些特性如下所示。
30.3.1 短期分析
乘数弹塑性分析和极限分析中使用的是相同的材料模型、网格、单元类型等,在两种分析中最终极限荷载的结果是相同的,详情见表30.1。
表30.1 不同网格单元和分析类型的短期极限荷载
| 网格单元 | 分析类型 | 极限荷载,kN/m2 |
| 2000个单元,6-高斯节点 | 乘数弹塑性分析 | 125.1 |
| 2000个单元,6-高斯节点 | 极限分析 | 125.2 |
| 2000个单元,下限解 | 乘数弹塑性分析 | 118.8 |
| 2000个单元,下限解 | 极限分析 | 118.8 |
| 2000个单元,上限解 | 乘数弹塑性分析 | 129.9 |
| 2000个单元,上限解 | 极限分析 | 130.0 |
在上述乘数弹塑性分析中,分别采用了单元数量为2000,单元类型为6-高斯节点、下限解和上限解。利用极限分析重新计算,得到了几乎相同的结果,稍有区别的是乘法弹塑性分析得到的位移约0.2厘米(见图30.2),但无法达到原则上的完全破坏的位移。然而,通过继续加载,极限分析得到的结构最终将被精确地复制。
从表30.1可以看出,之前采用6-高斯节点计算得到的结果大约处于上限解和下限解之间,因此可以认为结果是合理的。
30.3.2 长期分析
接下来考虑长期分析的情况,正如上面所讨论的,流动法则对破坏载荷和破坏前的位移都有影响。对于排水分析,当流动法则为关联时,极限分析和乘数弹塑性分析通常保持一致。然而,极限分析设置中选取的有效合理的参数,对于非关联乘数弹塑性分析中极限荷载的预估更合理,且通常偏保守(详见理论手册)。对于φ= 20°,ψ= 0,c = 10 kPa,Davis参数为(见材料手册):
![]() (30.1)
(30.1)
表30.2总结了使用这些参数以及之前获得的各种结果。首先,这证实了当流动法则为关联时,极限分析和乘数弹塑性分析得出了相同的承载能力;其次,当流动法则是非关联时,使用戴维斯参数的极限分析可以提供一个合理的,这种情况下比较保守的,对承载能力的预估。
表30.2 使用不同网格单元和分析类型的短期极限载荷
| 网格单元 | 流动法则 | 分析类型 | 极限荷载,kN/m2 |
| 2000个单元,6-高斯节点 | 关联 | 乘数弹塑性分析 | 459.6 |
| 2000个单元,6-高斯节点 | 关联 | 极限分析 | 460.4 |
| 2000个单元,6-高斯节点 | 非关联 | 乘数弹塑性分析 | 424.9 |
| 2000个单元,6-高斯节点 | 关联,Davis | 极限分析 | 400.6 |
30.4 总结
流动法则对于Mohr-Coulomb材料的影响概括如下:
在相同的材料参数和有限元模型的基础上,用极限分析和乘数弹塑性分析得到的极限荷载是相同的。
对于排水/不排水材料的短期分析,极限分析和乘数弹塑性分析得到的极限荷载是相同的。
对于长期分析,达到极限状态时的承载力和位移都受流动法则的影响;在标准极限分析计算中,可以用Davis参数预估流动法则对承载力的影响。
OptumG2中所有的有限单元适用于所有的分析类型,使用乘数弹塑性分析中的上限和下限单元,可以计算出系统的强度和刚度的边界。