14 数值优化

优化与计算极限分析之间的关联由来已久。实际上，所有计算极限分析程序都直接导致优化问题。但是使用最优化方法作为解决弹塑性问题的手段却不常见。

将优化算法应用于此类问题的想法至少可以追溯到1960年代Giulio Maier及其同事的工作（Maier 1968a，b，1984）。

有限单元法在涉及非线弹性、塑性、硬化等的非线性本构模型中的应用产生了非线性方程组。通常，必须在许多荷载步（如在静态弹塑性分析中）或时间步（如在固结分析中）的过程中解决这些问题。解决非线性有限单元的最常用方法方程是经典的牛顿-拉夫森方法。非线性方程在这里被线性化，并且通过迭代序列解决了一个类似于线性弹性的问题，直到收敛为止，即直到原始非线性方程满足某个指定公差。

在OPTUM G2中使用了不同的方法。与其直接求解非线性方程，不如解决等效的优化问题来满足原始方程的解。以非线性方程为例：

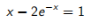(14.1)

牛顿-拉夫森方法在该方程式上的应用很简单，最终解x = 1.4630555。

相反，Optum方法将考虑优化问题：

最小化 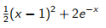 (14.2)

为了解决这个问题，我们区分目标函数（求导的函数）并将结果设置为零：

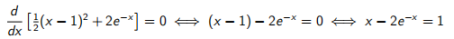(14.3)

公式可推出原始的非线性方程14.1。 接下来，可以继续选择任一方法，包括Newton-Raphson，来求解最终的方程式，即优化术语中的最佳条件。

对于这个特定问题，这两种方法是完全相同的。但是，对于更复杂的问题，在效率和精确度方面，优化方法通常在技术上优于传统方法。既包括弹塑性也包括极限分析的问题，优化方法是唯一可行的方法。

14.1算法

应用于极限分析的最早算法是为线性程序（LP）设计的。是能够解决以下类型的线性程序问题的算法：

最小化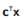 

满足 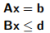   (14.4)

上限和下限分析都可以这种形式进行。在下限分析中，目标函数将包含荷载乘数，平衡方程用等式约束表示，屈服条件考虑用不等式约束。由于大多数实际的屈服条件是非线性的，因此必须先进行线性化，然后才能将问题设置为线性程序。虽然这样的线性化（根据需要在原始屈服面的内部或外部）很容易制定，但是早期的LP算法具有运行时间与约束数量成指数关系的特性。因此，当Karmarkar于1984年宣布发现多项式时间算法时，它被认为是一项重大突破（不仅在学术界，而且在主流媒体中，见图14.1）。尽管新算法及其在商业开发方面的潜力令人兴奋乃至大肆宣传，但很快发现它实际上与Fiacco和McCormick（1968）先前提出的所谓的顺序无约束求导技术密切相关。这些技术的显着特征是它们同样适用于线性和非线性编程，而较早的方法则在两者之间有明显的区别。这些见解决定了随后几十年该领域的许多研究。标记内点法是Karmarkar的一类算法，通常被认为已经彻底改变了数值优化领域（Wright 2004）。

内点法适用问题可以写为

最小化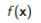 

满足 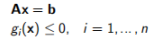   (14.5)

其中f和g通常被认为是凸的。

在进一步的发展中，意识到可以通过设计高效而强大，比最一般的凸面更严格的算法，提出了所谓的圆锥编程算法（例如参见Ben-Tal和Nemirovski 2001）。 圆锥形程序标准形式编写通常如下：

最小化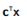 

满足 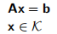(14.6)

其中K是一个圆锥体。 圆锥的示例包括二次圆锥：

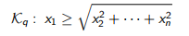(14.7)

正半定锥，其中变量的平方矩阵必须为正半定

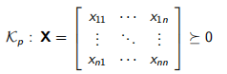(14.8)

这两个锥体对塑性方面有用—第一个用于二次屈服准则（例如Drucker-Prager）建模，而第二个可用于Mohr-Coulomb准则建模。

图14.1：与Karmarkar算法相关的新闻剪辑

（由RJ Vanderbei收集，http//orfe.princeton.edu/~rvdb/pdf/talks/pumath/talk.pdf）

比常规圆锥编程更专业化是仅考虑二次约束的二次锥规划（SOCP），即二次锥（14.7）和旋转的二次锥：

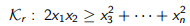(14.9)

OPTUM G2中包含的SONIC / Serial和SONIC / Parallel算法是SOCP算法。 有关将SOCP（以及一般圆锥编程）应用于可塑性问题的部分论文如下：

• Makrodimopoulos and Martin (2006, 2007): plane strain Mohr-Coulomb limit analysis using SOCP.

• Krabbenhoft et al. (2007a): limit analysis and elastoplasticity for plane strain Mohr-Coulomb problems, limit analysis and optimal design of reinforced concrete plates using SOCP.

• Krabbenhoft et al. (2008): 3D Mohr-Coulomb limit analysis using semidefinite programming.

• Krabbenhoft and Lyamin (2012): drained and undrained elastoplastic analysis of plane strain Modifified Cam Clay problems using SOCP.

• Krabbenhoft et al. (2012): nonassociated elastoplastic analysis using SOCP.

• Zhang et al. (2013): dynamic large deformation analysis and granular flows governed by MohrCoulomb using SOCP.

14.2非二次逼近

OPTUM G2仅使用SOCP。由于所处理的许多问题本质上并非都是二次的，这也构成了挑战。例如，Hoek-Brown标准不是二次方的。同样，修正Cam Clay模型的弹性法则和硬化法则也不都是二次方。但相对直接的是，用定点迭代序列解决所得的近似问题。为了说明典型过程，再次考虑问题

最小化 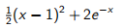(14.10)

第二个术语在这里是非二次的，不能直接使用SOCP处理。 而是考虑由二阶泰勒展开式给出的关于点x0的近似值

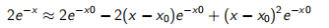(14.11)

这里有

最小化 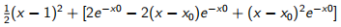(14.12)

这里可以使用SOCP解决。从x0 = 0开始，我们获得了解决方案

x = 1.0000000     (14.13)

接下来，设置x0 = 1并再次求解，得到解

x = 1.4238831     (14.14)

指定x0=1.4238831，使用此解决方案，得到

x = 1.4628094     (14.15)

依此类推，直到收敛到x = 1.4630555的正确解为止。