15 检验与校核

有限元软件用户面临的一个中心问题是，在多大程度上可以从面值获得结果，这在多大程度上代表了真实情况，又在多大程度上复制了著名的分析解决方案等。检验与校核（V＆V）概念的基本思想是帮助系统地回答这些问题。 V＆V已在产品设计和软件工程中得到广泛使用，并且近年来也已将其应用于材料力学，计算力学及相关领域。

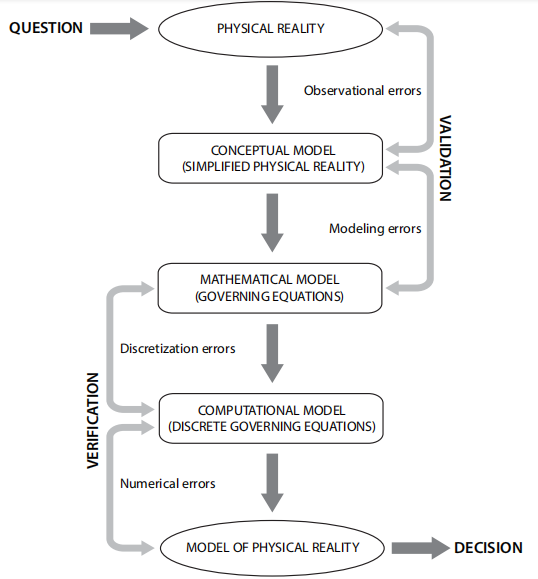
图15.1：数值分析使用逻辑

数值分析的使用首先提出一个相关的问题。 例如：给定地基的承载力是多少？给定基坑支护的板桩墙的尺寸应该是多少?……对这些问题做出答案并做出相关决定的过程是通常通过图15.1中概述的步骤顺序进行操作。

首先，包括建立概念模型，即物理模型的抽象和最终简化。在概念模型中，仅包括对我们最终想要描述的问题产生影响的物理因素。此外，概念模型的建立涉及收集和开展相关观察，例如关于在实验室测试材料参数、场地几何形状、地下水条件等。

其次，根据观察结果和可能更多的“基础”理论，建立数学模型。数学模型是指一组方程，这些方程至少可以获得可用的观察结果，并且有望进一步在经验范围之外做出有用的预测。对于固体力学问题，通常将包括平衡方程、应变位移关系和应力应变关系。接下来，是求解控制方程。这可以通过用离散对应项来近似原始控制方程的连续变量（位移，应力等）。在单元形状函数和离散节点变量的基础上对连续变量进行近似的有限单元法，提供了一种离散控制方程的方法。所得的离散方程组称为计算模型，并且在实践中必须通过数值求解。

最后，通过求解离散控制方程，我们得出一个解决方案，即一组应力，位移等，可以在此基础上做出进一步的判断。

V＆V思想是系统地评估该解决方案的有效性。尽管经常混淆，但验证和确认是两个独立的过程。在当前情况下，我们可以说这两个程序涉及以下问题：

检验：数学模型在模拟物理模型方面是否合适？

校核：构成数学模型的方程式是否正确求解？

要么：

检验：是否求解方程式是否正确的？

校核：方程是否正确求解？

重要的是要分别处理这两个问题，更笼统地说，要认识到最终解受数值解过程中几个不同阶段的误差影响。

15.1检验

检验与校核过程从最后开始，即从计算出的解决方案开始。首先必须确保实际上满足离散控制方程。尽管此任务相对简单（将解决方案简单地插入离散方程式中），但确保计算正确解却并非如此。实际上，与典型的地质力学问题相关的离散方程往往是高度非线性的，通常会涉及某些类型的奇点且常常不适用。这些难点是标准数值问题（例如截断和舍入误差）之外的。因此，单独求解离散控制方程的过程常常会导致误差显著。所以，大多数有限单元程序（包括OPTUM G2）都提供了有关最终解决方案精度的信息，并且具有用于检测最大误差的内置程序，最终由用户负责确保计算出的解满足离散控制方程的要求并处于可接受的公差范围内。

其次，通常更常见和更严重的错误是控制方程离散化导致的。使用标准有限元方法，关于固有误差的唯一真实信息是所计算的解不安全，即高估承载力而低估沉降。没有可靠的和通用的方法来估计误差的大小。因此，通常进行收敛分析，逐渐细化网格，直到观察到某些关键量（位移，反作用等）达到稳定值为止。尽管此过程在许多情况下是非常合适的，但它具有一定的局限性，其中最重要的是，达到收敛所需的有限单元数可能会非常大。类似地，必须注意确实达到收敛，解决方案被认为是收敛是指即从一个网格到下一个网格的变化率实际上足够小。

作为替代方法，在某些情况下可以构造有限元近似值，从而可以保证某些数量被低估或高估。这样的单元在OPTUM G2中，可用于计算岩土结构的承载力或安全系数的上限和下限。类似地，可以计算弹性能的界限，以获得“太刚”或“太柔”的解。 使用OPTUM G2，针对数学模型对计算模型进行的验证包括细化网格，直到认为上限解和下限解之间的间隙足够小为止。用L表示下限解，用U表示上限解，则精确解E的边界为

L ≤ E ≤ U       (15.1)

另外，真实解可以通过上下限之间的平均值来近似：

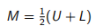(15.2)

有

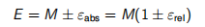(15.3)

其中ε_abs和ε_rel分别是绝对误差和相对误差，它们的范围是

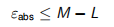(15.4)

和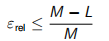(15.5)

例如，考虑一个宽度为B的条形基础，它受中心垂直荷载q，搁置在重度γ且摩擦角ϕ = 30°的纯摩擦材料上。对于此问题，真实承载能力为E = 2qu /Bγ= 14.75。假设已经计算出L = 12.0的下限和U = 17.0的上限。上限和下限之间的平均值为

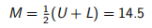(15.6)

相对误差

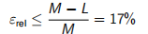(15.7)

换言之，真实解由

E = 14.5 ± 17% (15.8)

如该示例所示，上限和下限之间的平均值的实际误差比最坏情况下建议的要小得多。确实，平均值M = 14.5，精确解E = 14.75，实际误差仅为1.7％。实际上，上限和下限趋于以相同的速率收敛到精确解，即EEL≈UUE，使得即使是非常粗糙的网格E≈M = 1/2（U + L）通常是精确解的很好估算值。

15.2校核

校核旨在首先针对概念模型验证数学模型。为此，通常必须依靠不完整的观察结果，例如实验室实验中代表性土壤样品的响应，以及在施工阶段可能测量的变形，孔隙压力变化等。另外，应验证某些类型的预期响应。例如，距垂直荷载基础一定距离的表面沉降应趋于零。在将概念模型转换为数学模型时，一些较常见的模型错误包括：

•材料模型的缺陷

•初始应力分布不当

•初始孔隙压力分布不合适

其次，必须对概念模型本身进行审查，并与物理模型保持一致。相关问题包括：

•是否对某些观察结果有误判？

•概念模型是否太简单了？

•是否考虑了所有相关因素？

这些以及相关问题通常不容易明确地回答，并且不可避免地会涉及大量难以量化的判断。

15.3正确使用V＆V

上述“检验与校核”的关键特征在于，它有助于对从物理模型到数值解法的每一步中可能产生的误差进行严格的分析。特别要强调的是，不应将最终的数值解直接与物理模型进行比较。实际上，很可能在不同阶段产生的误差会相互抵消。例如，不合格的有限单元离散法与同样不合适的本构模型结合使用可能会产生比相同的本构模型中使用更高质量的有限单元离散法将更好的计算结果。正确使用V＆V会发现这种情况从根本上来说是不能令人满意的，只有在每个阶段中涉及的误差是可以接受的情况下，才可以认为解是可以接受的。