OptumG2考虑土体硬化的基坑分析

在基坑开挖过程中，实际上是一个土体卸载的过程，对于软黏性土会存在明显的土体硬化特征，且卸载过程中坑外和坑内的土体变形比较难合理考虑，因此在对基坑开挖进行数值模拟时需要准确的选取本构模型。

对于土体卸载回弹和再压缩的特性，如图1所示。土体从A点开始分级加载，压缩至B点后，分级卸载回弹至C点，再分级加载让土体压缩。在卸载时，土体不是沿着初始压缩曲线，而是沿曲线BC回弹，说明土体的变形是由可恢复的弹性变形和不可恢复的塑性变形两部分组成。回弹曲线和再压缩曲线构成一回滞环，这是土体不是完全弹性体的有一表征。在同样的压力范围内，回弹和再压缩曲线要比初始圧缩曲线平缓得多，说明在回弹或再压缩范围内，土的压缩性大大降低。当再加载时的压力超过B点所对应的压力时，再压缩曲线就趋于初始压缩曲线的延长线。

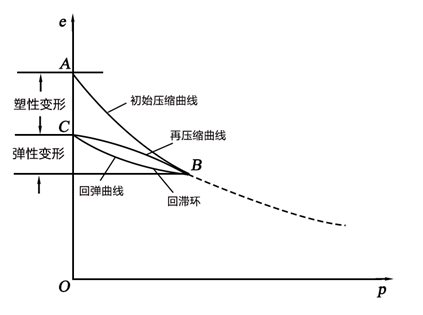
图1 土体的卸载回弹-再压缩曲线

由于土体不是完全弹性体，存在土体硬化的因素，在模拟基坑开挖过程的时候，墙体前面进行加载，墙后发生卸载，分析坑外和坑内的土体变形，考虑土体的卸载回弹是非常有必要的。因此，OptumG2软件中的HMC模型则非常适合，它能够分别运行初始弹塑性加载和后续的弹性卸载过程的刚度模量。

下面以OptumG2案例手册中的案例39为例，简单介绍一下HMC模型的应用。

模型中对砂土进行开挖，开挖时采用板桩墙对其进行支撑，如图2所示。安置好钢板桩之后，开挖过程为：第一步先开挖墙前4m，第二步再开挖4m，第三步先在地下2m插入支撑，之后再开挖4m，此时总的开挖深度为12m；第四步给支撑添加500kN/m的预应力；第五步再开挖4m，最终的总开挖深度为16m。

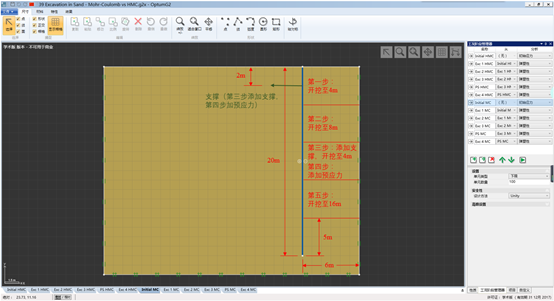
图2 模型及砂土开挖过程

为了测试土体的整体破坏模式对于本构模型选取的敏感性，特别是刚度模量的选择，在分析过程中分别采用了HMC模型和MC模型进行对比。HMC模型中采用的参考刚度模量E_50,ref = 25MPa，E_ur,ref = 125MPa，MC模型中采用的两个固定的杨氏模量E = 25MPa，E = 125MPa。关于两者采用的详细参数，如表1所示。

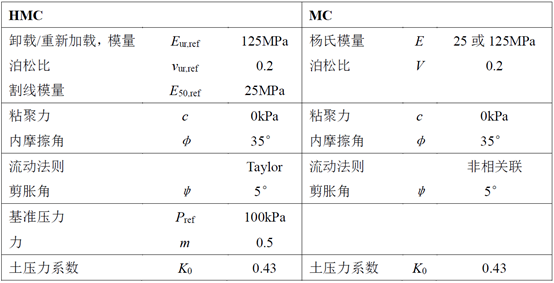
表1 HMC模型和MC模型的详细参数

对于HMC模型和MC模型，分析采用的方法是弹塑性分析，计算采用的网格数量均为1000，网格类型为6-高斯节点。

如图3和图4所示，为基坑开挖8m和12m之后的墙体位移和墙体弯矩，大体可以看出，不管土体采用的是HMC模型，还是不同参数的MC模型，墙体的位移和弯矩之间的差别很小，结果具有良好的一致性，即基坑开挖时，土体的模型选取对墙体的稳定性影响不大，对结构的影响作用很小。

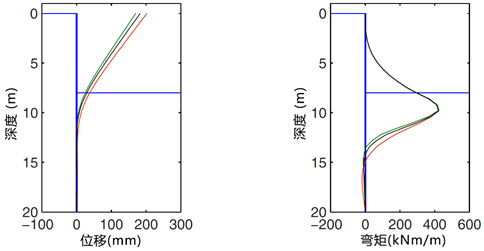
图3 基坑开挖8m后墙体的位移(左)和弯矩(右)

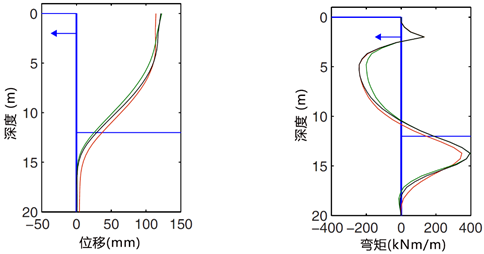
图4 基坑开挖12m后墙体的位移(左)和弯矩(右)

如图5所示，为基坑开挖4m后墙后和墙前的地表位移，总体来看，采用HMC模型和MC模型得到的结果差别比较明显。对于墙前的地表位移，开挖时墙前为加载过程，HMC模型与MC模型的结果一致，土体模量越大，墙前的位移也越大。对于墙后的地表位移，开挖时墙后为卸载的过程，HMC模型可以准确的显示离墙越远，地表位移越小的特性；而MC模型显示的墙后地表位移存在一个明显的拱起，模量越小拱起越明显，显然这是存在一定的问题的。

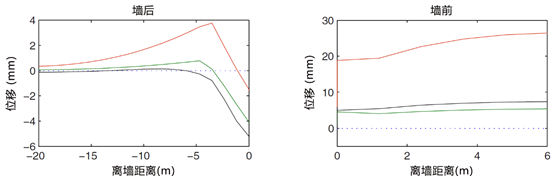
图5 基坑开挖4m后墙后(左)和墙前(右)的地表位移

对于基坑开挖问题，如果只是计算墙体，即结构稳定性的话，不管是采用HMC模型还是标准的MC模型，计算得到的结果都是没有问题的。但是如果要考虑土体的整体稳定性，需要采用HMC模型来进行计算，如果采用MC模型的话，由于基坑开挖过程是一个卸载的过程，土体存在一个回弹的过程，而MC模型在计算时是无法考虑这一因素的，因此计算得到的结果是不准确的，而HMC模型则会避免该因素的影响，进行准确的计算分析。